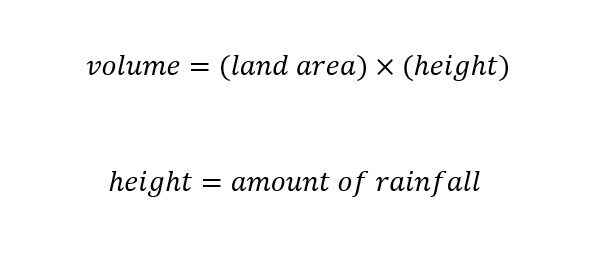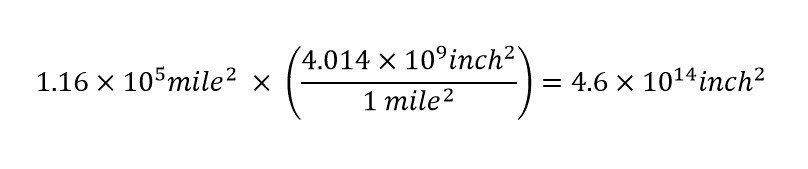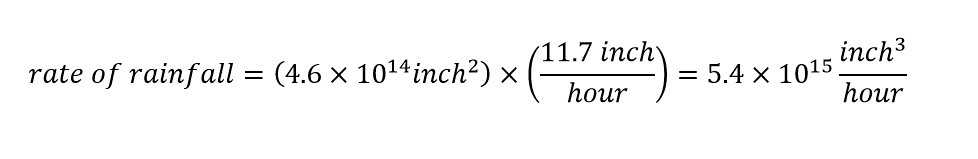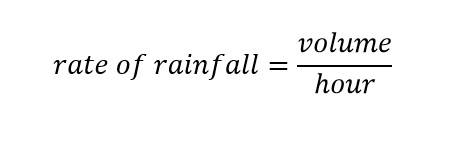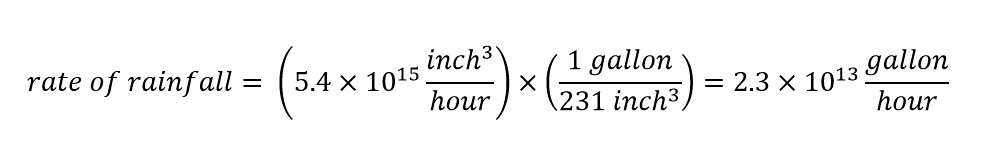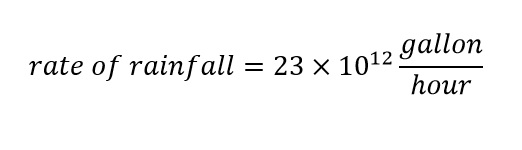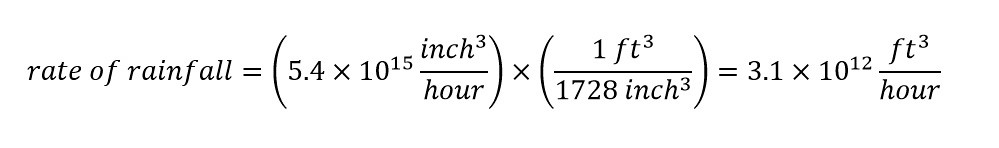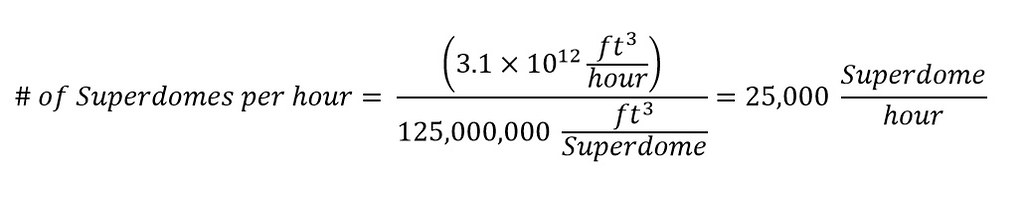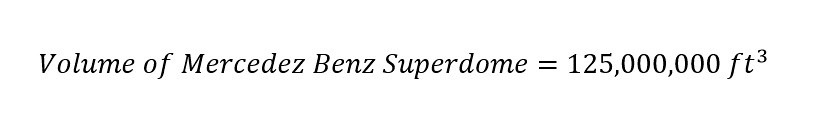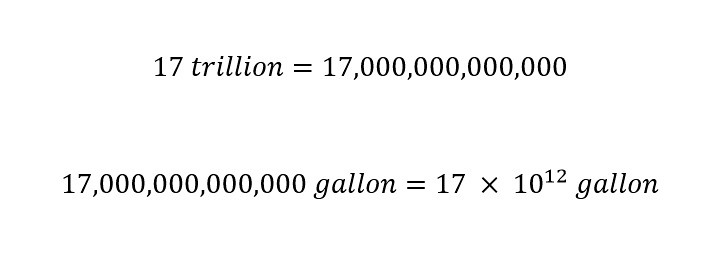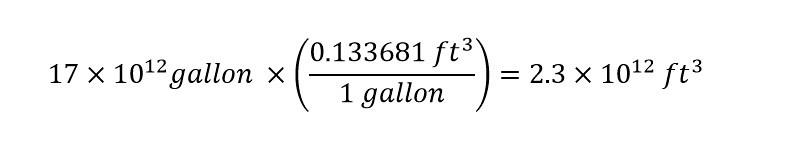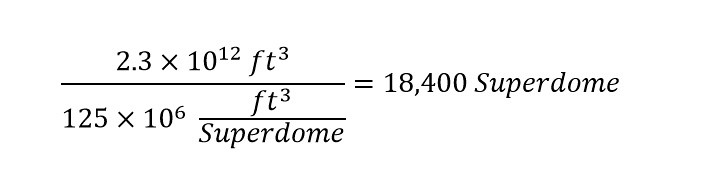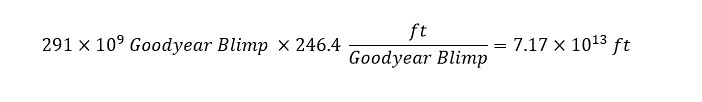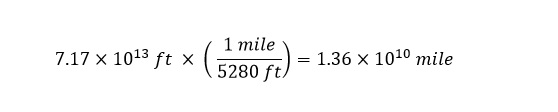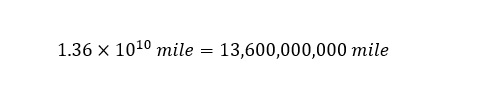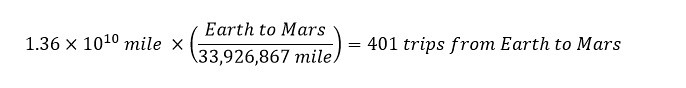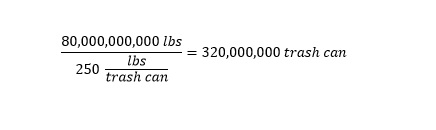Typhoon Mangkhut Drops Enough Rain On Philippines To Fill 25,000 Superdomes per hour?

Source: Time

As Americans were watching Hurricane Florence ravage the East Coast of the United States over the weekend, residents of the Philippine Islands were experiencing an equivalent destruction of their country from Typhoon Mangkhut.  According to the New York Times article titled "See Inside Typhoon Mangkhut in 3-D" at the height of maximum rainfall over the Philippines, the rate of rainfall reached 11.7 inches as shown in the excerpt below:

Rain tends to be heaviest near the center of a storm, in what is known as the eyewall, visible here in red. The highest rainfall rate for Typhoon Mangkhut reached 11.7 inches per hour inside the southern wall on Friday.

With this astounding rate of rainfall in mind, regular readers of this site will naturally ask themselves the following question:



How many Superdomes were filled per hour by Typhoon Mangkhut?



In the paragraphs below, the amount of Superdomes are calculated using dimensional analysis.  The result as indicated (potentially 25,000 Superdomes per hour) is astonishing.  Following the analysis is a video confirming the astounding number which should blow your mind.

How Many Superdomes Per Hour?

Basically, for the current blog post, the same methodology which was used to calculate the number of Superdomes which could be filled with the predicted rainfall due to Hurricane Florence - which I posted last Friday.  The Mercedes-Benz Superdome is located in Louisianna and has an interior volume of 125,000,000 cubic feet.  Shown below is a picture of the Mercedes-Benz Superdome:

Source: The Advocate

Superdomes can be a 'metric' which are commonly used to cast large (enormous) values of volumes or statistics popularly reported in the news.  The maximum rate of rainfall reported in the New York Times article above is a perfect candidate along with the landmass of the Philippine Islands -- which makes a volume -- to be used in an analysis with the metric above used.  The volume of rainfall can be expressed as an equation as shown below:

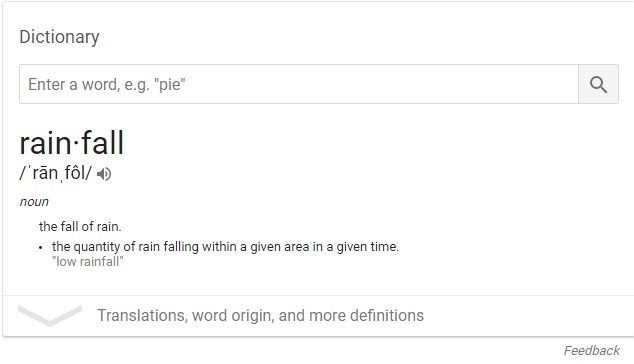
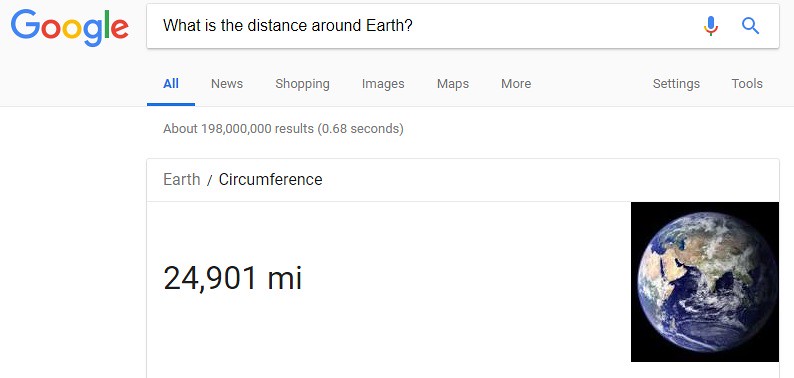
The volume for a geographic area is the land mass area multiplied by the amount of rainfall over the given land mass area.  If we consult Google with the following question: Rainfall?  The definition of the term 'rainfall' is shown below:

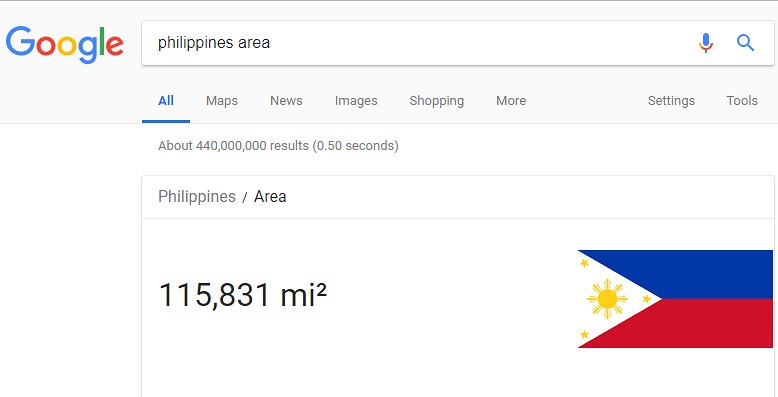
The definition of rainfall is 'the quantity of rainfall falling.'  To begin the analysis (with actual numbers) the land mass (total area) of the Philippine Islands needs to be determine.  As usual, Google is consulted with the following question: Philippine Area?   The answer is shown below:

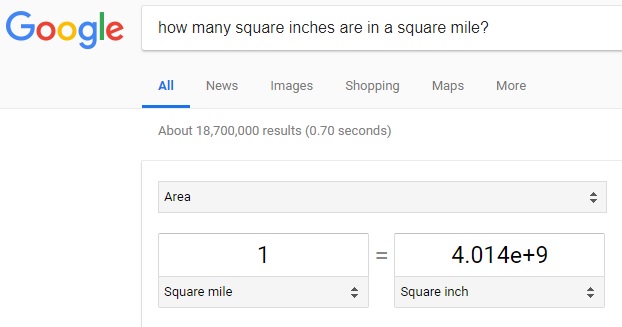
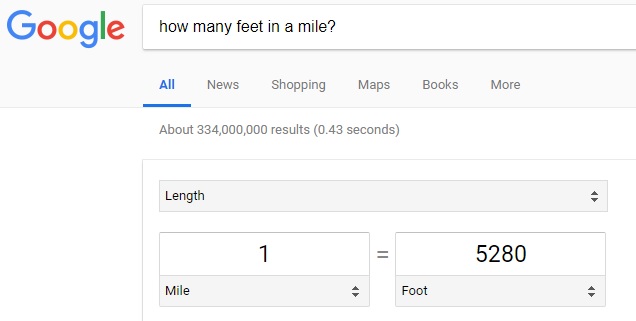
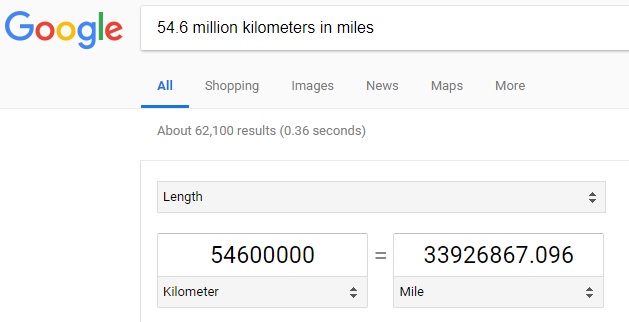
Notice that the area (land mass) is expressed in units of measurement of 'square mile'.  When the maximum rainfall is reported in units of 'inches', a decision to convert one number to the other needs to be made.  For this analysis, 'inches' will be the unit of measurement for analysis -- at least the beginning of the analysis.  In order to convert the land mass area of Philippine Islands from units of 'inch' to 'mile' the following question needs to be asked in a search engine like Google: How many square inches in a square mile?  The answer is shown below:

For every single square mile, there are 4.014 billion square inches.  The conversion of units from 'square miles' to 'square inches' is shown below:

The answer above shows that Philippines is around 116 thousand square miles which when converted to square inches turns out to be 460 trillion square inches.  Now that the land mass area is converted to units of square inches, the volume of rain which fell at a maximum on Friday due to Typhoon Mangkhut can be calculated using the expression for volume from above:

Wait?  The above equation is 'rate of rainfall' -- whereas I stated that the volume was being computed above?  Why the difference?  As I stated above, the amount of rain falling over and hour was reported to be 11.7 inches/hour.  Which is a rate.  Therefore, the volume is actually the rate of volume of rainfall over a given time as shown below:

With 11.7 inches/hour of rainfall pouring down due to Typhoon Mangkhut, the total amount (volume) of rain would be 5,400 trillion cubic inches per hour of rain.  Wow!  Based on the calculations in the previous blog post regarding the total amount of rain predicted (by a forecaster) due to Hurricane Florence, lets cast the rate of rainfall into comprehensible units.  To do so, a unit conversion needs to be accomplished from units of 'cubic inches' to 'gallons'.  A conversion factor needs to be determined.



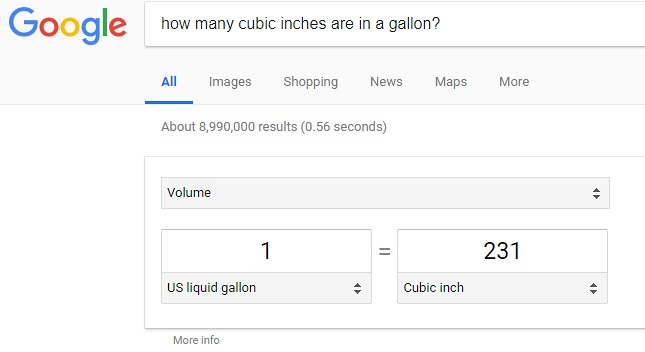
If the following question is typed into Google: How many cubic inches are in a gallon?  The answer is shown below:

With the conversion factor known, the conversion is carried out by using the same methodology as above:

Therefore, the amount of rainfall over the Philippine Islands at maximum rainfall is shown below:

Wow!  23 trillion gallons in a single hour.  In my previous blog post about the predicted amount of rainfall over four states (in a few days) was expected to be 17 trillion.  The difference shows that Typhoon Mangkhut is larger than Hurricane Florence.  This is not to say that Hurricane Florence is not inflicting a large amount of damage in the United States over the weekend.  The East Coast is in terrible shape and we are keeping the residents there in our thoughts.  Be safe.



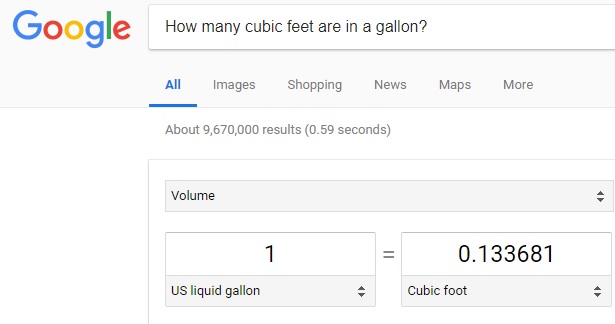
The metric which has been used to visualize large volumes of rain is the Mercedes-Benz Superdome as shown above.  With a volume of 125,000,000 cubic feet, the Superdome is a perfect metric to which compare the large volume of rain falling over a given region in a storm.  To calculate the number of Superdomes which could be filled with 23 trillion gallons/hour, first a unit conversion needs to be accomplished.  In order to compare the 23 trillion gallons/hour to 125,000,000 cubic feet, a unit conversion from 'gallon/hour' to 'cubic feet/hour' needs to be accomplished.



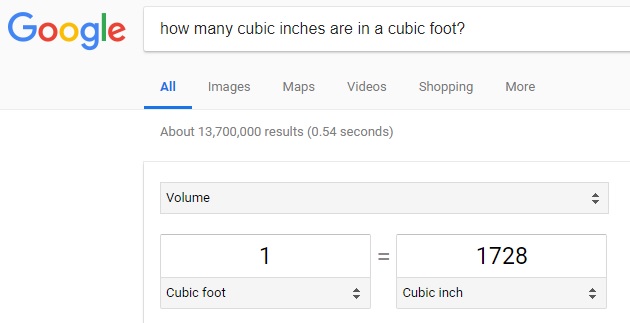
To determine the number of 'cubic inches' are in a 'cubic feet', we type into Google the following question: How many cubic inches are in a cubic foot?  The answer is shown below:

The conversion of units between 'cubic inch' and 'cubic feet' is shown below:

Next, to determine the number of Superdomes which could be filled with the amount of rain falling over an hour over the Philippine Islands is shown below:

Wow!  The total amount of Superdomes which would be filled at the rate of rainfall equal to 3.1 trillion cubic feet per hour is a whopping 25,000 Superdomes per hour.



The final question is the following:



Does the amount of rainfall -- 3.1 trillion cubic feet per hour over the Philippine Islands make sense?



To answer the question above, lets view the video from YouTube below taken over the weekend during the storm - Typhoon Mangkhut:

Wow!   I am left speechless by the video above.

Conclusion...

Oh my goodness?  The amount of rain is enormous and unparalleled.  Between the total number of storms hitting the globe over the weekend, the amount of rainfall is historic and unparalleled in volume.  The rainfall must be surging into the hundreds of trillions of gallons of water falling on land masses like Philippine Islands and the East Coast of the United States of America.  Destruction is inevitable.  Just think of the amount of time and effort which will be required to restore basic resources like power and water?  The destruction is huge and should not be understated.  Keep the residents experiencing these terrible storms in our thoughts and prayers.



Related Blog Posts:


A Forecaster Predicts That Hurricane Florence Will Drop Enough Rain To Fill 18,400 Mercedes-Benz Superdomes

Hurricane Harvey Drops Enough Rain On Houston To Fill 560 Dallas Cowboy Stadiums

How Much Water Is Contained In All Oceans Around The Globe?

Storm Raises Water Level In Lake Cachuma By 31 feet, How Much Water Is That?

How To Make Sense Of Water Flowing At 100,000 Cubic Feet Per Second

Can 11 Trillion Gallons Of Water Fill 14,000 Dallas Cowboys Stadiums?

How Much Rain Did The East Coast Receive From Hurricane Matthew?


How Much Rain Did Haiti Really Receive?

How Much Rainfall Has Dropped On Louisiana?


How Big Was The "Water Bomb" Of Rainfall In Macedonia?

How Much Rain Did Huauchinango (Mexico) receive?

How Much Rain Did Elliot City (Maryland) Really Receive?

If The Mosul Dam Breaks, The City Of Mosul Would Be Under 65 Feet Of Water?

What is the volume of water in a few inches of rain?


Volume of Waste in the Mine Spill (in Brazil) Equivalent to 78 Deepwater Horizon Oil Spills

A Forecaster Predicts That Hurricane Florence Will Drop Enough Rain To Fill 18,400 Mercedes-Benz Superdomes

Source: Axios

Hurricane Florence has arrived on the East Coast of the United States with a force which seems unparalleled compared to previous storms.  The category has changed with time, though, without dispute, hurricane Florence is present and causing damage which will take years to recover from.  To comprehend the predictions from weather forecasters, dimensional analysis is necessary to cast the enormous predictions into light.  How much rain is going to fall on the East Coast from hurricane Florence?  Here is an excerpt from a weather forecaster interviewed by 'Mashable' in an article titled "Hurricane Florence is forecast to dump a historic amount of rain. Here's how much" which states the huge amount of potential rain to be dropped:

Meteorologist Ryan Maue of WeatherModels tweeted some projections on Thursday morning. 

Maue's models suggest that around 17 trillion gallons of rain will fall across North Carolina, South Carolina, Virginia, and Georgia with some spots receiving as much as 30 inches of rain before Florence is finished. 

According to the excerpt shown above, 17 trillion gallons is predicted to fall on North Carolina, South Carolina, Virginia, and Georgia over the next few days.  This will cause terrible damage to the infrastructure in cities lining the coast and displace many thousands of residents from services (which are much needed) such as electricity, emergency services, and make returning to work nearly impossible.  In order to understand the terrible destruction of the storm, the amount of rain (17 trillion) should be placed into context.  In the paragraphs below, dimensional analysis is used to compare the amount of rain to the number of Mercedes-Benz Superdomes which could be filled with 17 trillion gallons.

How Much Space Occupies The Mercedes-Benz Superdome?

The metric which has been chosen to compare the enormous amount of rain that is expected to fall over the 4 states mentioned above on the East Coast over the next few days is the Mercedes-Benz Superdome.  The Superdome is located in Louisianna and has an interior space (volume) equal to 125,000,000 cubic feet of space.  Yes, I said 125,000,000 cubic feet of space as shown below:

Which fills the Superdome shown below:

Source: The Advocate

That is an large space indeed.  Football games are played in the Superdome and at max capacity will hold a total of 73,000 people.  Although, during a super bowl, the capacity has expanded beyond capacity to hold upwards of 79,000 people.  Needless to say, when an HUGE volume is reported of liquid such as the amount of rain which will fall over the next few days, a perfect metric to compare is that of the Mercedes-Benz Superdome.



According to the excerpt taken from the news, the amount of rain expected to fall is 17 trillion gallons.  First, lets look at the amount of zero's after 17 -- trillion.  If 'Wikipedia' is consulted for the page defining 'trillion', the following definition is shown below:

Trillion (short scale) (1,000,000,000,000; one million million; 1012; SI prefix: tera-), the current meaning in both American and British English.

Therefore, if the number 17 trillion is written out in entirety, the number would appear as follows:

The first line above shows 17 trillion in long form.  For the purpose of shortening up a number to move around in calculations used in dimensional analysis, the value 17 trillion could be expressed in 'Scientific Notation' as shown in the second line above.  Which makes writing and expressing the number much easier.  Compared to writing out all of the unnecessary zero's involved.



Notice that the unit of measurement in which the amount of rain projected to fall are expressed in units of 'gallons'.   Remember that the interior space of the Superdome is expressed in units of 'cubic feet'.  Therefore, if the two numbers are going to be used in the same analysis (the purpose of the blog post), then a 'unit' conversion is necessary.  For this blog post, I will arbitrarily use the units of 'cubic feet' as a comparison.  We just as well could have converted over the units of 'cubic feet' to 'gallon's in order to compare the two values of interest (i.e. volume of Superdome and volume of rain).



In order to convert the units of measurement from 'gallon' to 'cubic feet', a conversion factor is needed.  To simplify the search for a conversion factor, consult Google with the following question: How many cubic feet are in a gallon?  The answer is shown below:

For every gallon, there are 0.133681 cubic feet.  Written as a conversion factor, the unit conversion from gallon to cubic feet is shown below:

The answer to the conversion shows that 17 trillion gallons is equivalent to 2.3 trillion cubic feet.  Which means that 17 trillion gallons of water is equivalent to 2.3 trillion cubic feet of water.  Same volume, different units of measurement. Now that both values are in the same units of measurement -- 'cubic feet' -- a simple division of two values (total volume of rain divided by total volume of a single Superdome) yields the total number of Mercedes-Benz Superdomes which would be filled with 17 trillion gallons of rain:

The answer indicates that if 17 trillion gallons were poured into 18,400 Superdomes, there would be no water remaining.  Wow.  With this enormous amount of Superdomes as a result, there should be no wonder why residents should be concerned about their health and safety.  That enormous amount of rain will inevitably wreak havoc on the four states listed above.

Conclusion...

In the blog post above, the number of Mercedes-Benz Superdomes were calculated which would be needed to hold a total volume of rain of 17 trillion gallons.  At this moment, you may be wondering how 17 trillion gallons compares to the amount of rain that Hurricane Harvey dropped on Houston (Texas).  Hurricane Harvey dropped 58.3 billion cubic feet of rain.  That is enough to fill 560 Dallas Cowboy Stadiums.  Note that the total amount of rain is distributed across very different amounts of land masses.  Different amounts of rain across different proportions of land.  Still, these hurricanes are dropping enormous amounts of water (in the form of rain) which is wreaking havoc on the surrounding land.



Hopefully, the blog post above along with other dimensional analysis blogs on this site shed light on the severity of storms hitting the world over the past two years.  In the index of blogs below, other storms have been analyzed in a similar fashion.  Regardless of the size of the storm, any loss of life is tragic and unacceptable.  Please keep the residents of hurricane Florence in your thoughts over the next few days (and months).  If you are in the path of hurricane Florence, stay safe please.



Related Blog Posts:


Hurricane Harvey Drops Enough Rain On Houston To Fill 560 Dallas Cowboy Stadiums

How Much Water Is Contained In All Oceans Around The Globe?

Storm Raises Water Level In Lake Cachuma By 31 feet, How Much Water Is That?

How To Make Sense Of Water Flowing At 100,000 Cubic Feet Per Second

Can 11 Trillion Gallons Of Water Fill 14,000 Dallas Cowboys Stadiums?

How Much Rain Did The East Coast Receive From Hurricane Matthew?


How Much Rain Did Haiti Really Receive?

How Much Rainfall Has Dropped On Louisiana?


How Big Was The "Water Bomb" Of Rainfall In Macedonia?

How Much Rain Did Huauchinango (Mexico) receive?

How Much Rain Did Elliot City (Maryland) Really Receive?

If The Mosul Dam Breaks, The City Of Mosul Would Be Under 65 Feet Of Water?

What is the volume of water in a few inches of rain?


Volume of Waste in the Mine Spill (in Brazil) Equivalent to 78 Deepwater Horizon Oil Spills

Reader Question: How far would 291 billion Goodyear Blimps reach end to end?

Source: LinkedIn Learning

Recently, I had a reader respond on Facebook to a blog post titled: With 29 Trillion Cubic Feet of Natural Gas, How Many GoodYear Blimps Could Be filled? as shown below:

According to the image above, the reader asks the following question: How far would 291 billion Goodyear Blimps reach end to end?   In the blog post below, the answer will be revealed in comparison to three distances:

1) Would the distance be enough to travel around planet Earth?  

2) Would the distance reach from the Earth to the Moon?

3) Would the distance reach from the Earth to Mars?

The answers are outlined and solutions shown below.  Enjoy!

Line up 291 billion Goodyear blimps

In order to start the analysis above up, we need to refer to the 'data' page for the Goodyear Blimps which I provided from the last post -- which can be found here.  If the overall length is searched for on the web page, the answer is the length of a Goodyear Blimp is 264.4 feet long or 81% of the length of a football field.  Wow!  That is shown below:

With this number representing a single blimp, the total distance asked by the reader above can be found by simply multiplying two values together.  The first is the total amount of Goodyear Blimps by the length of a single Blimp (the second value) as shown below:

Obviously, the resulting distance is very long considering that a single blimp is around 80% of the length of a football field.  That is, the total length expressed in units of 'feet' is 71,300,000,000,000-feet.  Or 71.3 trillion feet long.  For distances that are expressed in units of feet that are so enormous, converting the unit into a larger unit (say a mile) makes sense for dimensional analysis.  Especially when the metric will most likely be expressed in units of 'mile'.

To do so, we need to know the amount of feet which are in a mile.  The answer can be found by asking a search engine like 'Google.com' the following question: How many feet are in a mile?  The answer is shown below:

The answer indicates that for every mile, there are 5,280 feet.  With that conversion value in mind, the following unit conversion from feet to miles can be accomplished as shown below:

The number of total miles which would be reached if 291 billion Goodyear Blimps were lined up end to end would be around 13.6 billion miles in total distance.  That number is shown below:

The only remaining question is how to make sense of such a large number?  What is an appropriate metric to use for comparison?  How about if we choose the following three distances:

1) Trips around planet Earth

2) Trips from planet Earth to the Moon

3) Trips from planet Earth to the planet Mars

Lets see how these distances compare to 13.6 billion miles.

1) Trips around planet Earth:

To find out how 13.6 billion miles compares to the number of possible trips around Earth, the circumference of Earth needs to be known.  The fastest way to obtain the circumference is to ask Google the following question:  What is the distance around Earth?   The answer is shown below:

Once we have an answer -- which is 24,901 miles around Earth, a quick inspection is performed to make sure units of measurement are the same.  Yes, both values, 13.6 billion miles and 24,901 miles are both expressed in units of 'mile'.  Therefore, dividing the total number of miles which equates to lining up end to end 291 Goodyear Blimps by the distance around Earth will yield the number of trips that would be made possible as shown below:

Wow!  The answer indicates that with 13.6 billion miles, we could travel around Earth 546,000 times.  Wow!

2) Distance from Earth to the Moon:

The last analysis of distances -- using the circumference around the Earth -- gave us a large number: 546,000 trips around the Earth.  I do not know about you, but trying to imagine that number is too difficult for me.  Therefore, a new metric needs to be created in order to make sense of this enormous number -- 13.6  billion miles -- with which we are left with to untangle.



Another possible metric would be to use the distance between Earth and the moon.  If Google is consulted by asking the following question: How far is the moon from earth? -- then the answer below appears:

From the last analysis, the remainder of the calculation is straightforward as shown below:

According to the calculation above using the numbers mentioned, the total number of trips from Earth to the Moon would be approximately 56,900 one way trips.  Wow!  Looking at the answer, the number of trips is still quite large.  Lets consider a larger metric -- the distance to Mars for a final analysis.



3) Distance between Earth and Mars:



As a final analysis, a yet larger metric is chosen -- which is the distance between Earth and Mars -- to cast the enormous distance of 13.6 billion miles into perspective.  Again, to start the analysis, the distance from Earth to Mars needs to be obtained.  Using the handy search engine Google with the following question: How far is Mars from Earth? -- will yield an answer: 

The answer gives us a slight problem.  Following a quick inspection of 'units of measurement', the answer is given in units of 'kilometers' whereas the distance which is used in the above analysis is expressed in units of 'miles'.  Therefore, Google needs to be consulted with the following question: 54.6 million kilometers in miles -- which yields the following conversion shown below:

Notice how usually the inquiry for unit conversion entails getting a conversion factor.  In this case, the distance of concern was in question to save time.  Now, the final analysis can be carried out -- which is to find the number of trips from Earth to Mars that would be made possible using the distance of 13.6 billion miles.  The analysis is shown below:

The calculation indicates that 401 trips would be possible between Earth and Mars.  Wow!

Conclusion...

In the analysis above, the question from a reader was entertained: how far would 291 billion Goodyear Blimps reach end to end?  The answer was astounding.  Much longer than I even imagined.  Although, using dimensional analysis allowed us to cast the value (i.e. total distance) into a manageable perspective.  The metrics chosen were distances within our galaxy.  If larger metrics were needed for an extremely larger number, the a 'light-year' could have been chosen to which compare astronomically large numbers too.  In the future post, there will be such large numbers which require truly long distances.



For the time being, I am thankful to the reader Mike Martino for asking such a great question.  I have had a wonderful time making sense of the distance calculated along with walking readers through the analysis.  Now, powered with the ability to perform similar analysis, choose different metric and arrive at different answers.  Use the numbers above to explore different analyses.  Feel free to comment on different analyses in the comment section below.



Related blog posts:



Dimensional Analysis Of Statistics And Large Numbers - Index Of Blog Posts


What is dimensional analysis?


How many trash carts can be filled with 80 billion pounds of trash?


How many people would be killed if 1,485 pounds of Fentanyl were distributed onto the streets in the U.S.?

What Is Dimensional Analysis?


Was The Recent Oil Spill in China The Largest In History?


LimeBike Dockless Bikeshare Riders Travel A Distance Of 13,000 Miles In Just Over 3 Weeks?

How Many Cigarettes Can You Roll With 18,000 Pounds Of Marijuana?


How Many Turkey's Are Served On Thanksgiving Day? How Many People Served?


How Much Trash Would Be Required To Fill The Great Wall Of China?


How Many Birds Per Minute Can Be Processed On A Single Line At A Poultry Processing Plant?


Hurricane Harvey Drops Enough Rain On Houston To Fill 560 Dallas Cowboy Stadiums

If Technology Fails, Use Basic Math Skills - Count Manually!!

How Much Water Is Contained In All Oceans Around The Globe?

How many trash carts can be filled with 80 billion pounds of trash?

Source: Saumya Khandelwal -- The New York Times

Each of us generates trash throughout each day.  The usual routine is to make sure that the trash that each of us generate ends up in 'the trash can' in each room.  From there, we know that the trash that is deposited will then get shipped to either a dump or a boat to another country.  Did you know that?  What if other countries cannot except anymore trash?  Why do I ask this question?  Read onto find out.



Recently, in an article in The New York Times titled "‘The Dump Killed My Son’: Mountains of Garbage Engulf India’s Capital" the author reported two stunning statistics regarding gigantic trash piles which were looming close to neighborhoods and carrying the possibility of transmitting disease.   Here is an excerpt which caught my eye regarding total amount of waste:

In the metropolitan area of Delhi, which includes the capital New Delhi, trash heaps are towering monuments to India’s growing waste crisis. About 80 billion pounds of trash have accumulated at four official dumping sites, on the fringes of a capital already besieged by polluted air and toxic water, according to the supervisors of the dumps.

Some of these dumps are simply open aired rooms which span up to 17 stories in height.  Yes, that is equivalent to around 170 feet in height.  WOW.  The weight in trash was another mind blowing statistic which was too much to comprehend.  Therefore, I decided to carry out a little dimensional analysis in order to better understand this mind blowing number -- 80 billion pounds of trash.  I asked the following question:



How many trash carts could be filled with 80 billion pounds of trash?

How many pounds of trash in a trash cart?

In order to start the analysis, the metric which will be used to cast this enormous number needs to be known.  The trash cart of interest is shown below:

This trash cart is commonly used in the United States by various waste management corporations.  The average amount of trash in pounds which each can hold might be tricky to figure out -- since not all trash weighs the same or takes up the same volume -- not all trash has the same density!



To get an answer, Google can be consulted by inserting the following question: "how many pounds of trash does a 96 gallon trash cart hold?"  The answer is shown below:

According to text in image, a 96 gallon trash can is able to hold up to 250 lbs of trash.  As I just mentioned, the exact amount of trash (weight) is difficult to calculate for a given volume.  Trash might weigh different amounts depending on the composition of the trash.  At this point, you might be a little disappointed.  No worries.



A common theme in this blog site is to "approximate" an answer.  Which is what is being done by us when we consult Google.  With an answer obtained, the analysis may be carried out to obtain a final answer.  With this in mind, lets move on to calculate the total amount of trash cans which may be filled with 80 billion pounds of trash.

How Many Trash Bins Hold 80 Billion Pounds Of Trash?

In the last section, the amount of trash was determined (in weight) which each trash bin (or can) could hold.  Given now the enormous statistic of 80 billion pounds -- the amount of trash in four different sites within the city Delhi, how many trash bins would be required to hold all of that trash?



The calculation can be done in a single step once the values (or numbers) and units of measurement have been inspected to ensure uniformity.  By uniformity of units, we mean that if a number such as the total amount of trash is reported in 'units of pounds', then our conversion factor must also be expressed in 'units of pounds' -- which is the case.



In the paragraphs above, the conversion factor for the 'density' of trash was determined by asking the search engine Google.  The density of trash was determined to be (approximated to be) around 250 pounds/96 gallons.  Density traditionally is expressed in units of 'grams/milliliters or kilograms/cubic meter.  For the sake of the current analysis, we can choose the units - we wish - as long as the answer is expressed in units typical for density.



Since a single 96 gallon trash can (or bin) holds around 250 pounds of trash, the density can be expressed as follows:

We drop the 96 gallons and substitute 'per trash can' -- meaning 1 trash can = 96 gallons.  Yes, volume is expressed as a single trash can -- strange.  This is acceptable as long as we state our assumption explicitly for the reader.  Therefore, the total amount of trash cans needed to hold 80 billion pounds of trash is calculated by dividing the total amount of trash by the density of trash as shown below:

The answer indicates that a total of 320,000,000 trash cans or 320 million trash cans.  Wow!  Not a small amount.  Naturally, when I read a startling statistic like this, I wonder why such an enormous amount of trash has been allowed to accumulate over time?  What about the propagation of disease?  Is there a possibility of disease propagation with such a staggering amount?



In another section of the same article, the description of a single pile was 17 stories high?  That is over 170 feet tall (an approximate value) as mentioned above.  Wow.  Now that the following analysis has been performed, you (the reader) have been liberated to carry out similar analyses using the same method.  In addition, analyses such as the one above shed a greater amount of light on the magnitude of the problem at hand -- the accumulation of trash.



Related Blog Posts:



How many people would be killed if 1,485 pounds of Fentanyl were distributed onto the streets in the U.S.?

What Is Dimensional Analysis?


Was The Recent Oil Spill in China The Largest In History?


LimeBike Dockless Bikeshare Riders Travel A Distance Of 13,000 Miles In Just Over 3 Weeks?

How Many Cigarettes Can You Roll With 18,000 Pounds Of Marijuana?


How Many Turkey's Are Served On Thanksgiving Day? How Many People Served?


How Much Trash Would Be Required To Fill The Great Wall Of China?


How Many Birds Per Minute Can Be Processed On A Single Line At A Poultry Processing Plant?


Hurricane Harvey Drops Enough Rain On Houston To Fill 560 Dallas Cowboy Stadiums

If Technology Fails, Use Basic Math Skills - Count Manually!!

How Much Water Is Contained In All Oceans Around The Globe?

What Is Dimensional Analysis?

Source: Singularity Hub

What is dimensional analysis?  Have you ever used dimensional analysis in your everyday life?  Here is the introductory description which is located on the Wikipedia page for "Dimensional Analysis":

In engineering and science, dimensional analysis is the analysis of the relationships between different physical quantities by identifying their base quantities (such as length, mass, time, and electric charge) and units of measure (such as miles vs. kilometers, or pounds vs. kilograms vs. grams) and tracking these dimensions as calculations or comparisons are performed. Converting from one dimensional unit to another is often somewhat complex. Dimensional analysis, or more specifically the factor-label method, also known as the unit-factor method, is a widely used technique for such conversions using the rules of algebra.[1][2][3]

The concept of physical dimension was introduced by Joseph Fourier in 1822.[4] Physical quantities that are of the same kind (also called commensurable) have the same dimension (length, time, mass) and can be directly compared to each other, even if they are originally expressed in differing units of measure (such as inches and meters, or pounds and newtons). If physical quantities have different dimensions (such as length vs. mass), they cannot be expressed in terms of similar units and cannot be compared in quantity (also called incommensurable). For example, asking whether a kilogram is greater than, equal to, or less than an hour is meaningless.

Any physically meaningful equation (and likewise any inequality and inequation) will have the same dimensions on its left and right sides, a property known as dimensional homogeneity. Checking for dimensional homogeneity is a common application of dimensional analysis, serving as a plausibility check on derived equations and computations. It also serves as a guide and constraint in deriving equations that may describe a physical system in the absence of a more rigorous derivation.

Wow!  Does that sound complicated?  Basically, what the description says above is that if you are comparing the mass of two oranges, both the units of measurement (weight) in this case have to be in the same 'units' - grams, pounds, kilograms, etc.  If you weight orange number #1 and report a weight of 70 grams, then try to compare a second orange's weight reported as 0.400 kg (kilograms) - then the comparison cannot be completed.



At least until you convert the weight of orange #1 to units of kilograms or weight #2 to units of grams.  If both weights were expressed in the same units -- say grams, then orange #1 weighing = 70 grams -- would be much smaller than orange #1 weighing = 400 grams.  The same logic applies to base quantities (dimensions) -- like length, mass, volume, height, speed, etc.



How about trying another route to clarify the description in the excerpt above.  If you have ever tried to follow a recipe while cooking, then chances are you have engaged in 'dimensional analysis' without knowing that you were doing so.  Don't believe me? Follow the quick cooking example below.

Example: Cooking

Here is a quick example of using 'dimensional analysis' in your kitchen.  Take the recipe shown below as an example:

The recipe above calls for 100 mL of milk.  That is 100 milliliters of milk.   What if the kitchen in which you are preparing the shake does not contain a 'measuring cup' shown below which is extremely useful in converting between different units of measurement:

Source: HomeDepot

Upon closer inspection of the image of a 'measuring cup' above, one can easily see a series of markings at different heights with different labels.  These labels indicate different volumes of measurement in different units.  According to the image of the recipe shown earlier, the amount of milk called for in creating the shake was 100 mL -- Which could easily be converted using the instrument above -- i.e. measuring cup.



Although, what would you do if you did not have a measuring cup within the kitchen in which preparation of the shake was taking place?  How would a person find the conversion factor to convert between units of 'milliliters' and units of 'cups'?  One easy method with the advent of the internet has been to resort to to a 'search engine' like 'Google' or 'Bing'.



Proceed to bring up a web browser and bring up Google.com and type in the search space: "How Many Milliliters In A Cup?" and the web page with the conversion (interactive) columns should appear as shown below:

Note: The conversion shown above is 'interactive' - which means that the labels are 'drop down' menus which can serve to change either 'units of measurement' or 'dimensions' (i.e. length, area, volume, time, speed, etc.).  Feel free to play with the web page to convert between units of various dimensions.



Next, with the conversion factor known which will assist us in converting between units of 'cups' and units of 'milliliters', the remaining step in the conversion is to carryout a mathematical operation as shown below:

The result indicates that in order to follow the recipe (approximately -- not precisely), roughly 1/2 cup of milk will correspond to 100 milliliters of milk.  Note that the conversion is approximate -- since 1/2 = 0.5 not 1/2 = 0.423 !!!



Is the method of carrying out a dimensional analysis problem is clear?  If the answer is yes, then you are ready to read past blog posts which mainly use 'dimensional analysis' to cast statistics reported in the news into perspective -- click here to access the index of past blog posts.  If you are not comfortable with carrying out 'dimensional analysis' problems, see the tutorial below.

Dimensional Analysis Tutorial

A Tutorial on Dimensional Analysis is shown below:

After watching the video above along with reading the content of the blog post so far, you may be wondering where to get conversion values if not from the internet.  Science textbooks have conversion tables.  After a quick search of conversion tables, the 'Accidental Scientist' appeared with a host of information.  Here is a screenshot of an example of a table of conversions below.  Note: if you click on the source, you will be directed to the site:

As you can see, there is no need to memorize conversions -- at least all of the conversions.  That is what reference materials are for when needed.

Conclusion...

In the paragraphs above, the useful (and fun) method of carrying out calculations using 'dimensional analysis' was shown.  Armed with the power to carry out comparisons with conversion factors allows you to verify a large portion of statistics which are reported in the popular news on a day-to-day basis.  Is this useful?  Depends on how much energy that you choose to exert in understanding the process of using it to live a better life.


Understanding the power of comparison with conversion factors will add extra dimensions of happiness to your life.  How do I know?  When a person can visualize or comprehend the magnitude of a reported statistic by putting the value into perspective using dimensional analysis, the problem or subject matter of the news article becomes that much more useful to the reader.  Again, thank you for visiting the website and check out the dimensional analysis blog posts by clicking here.



Related Blog Index:


Dimensional Analysis Of Statistics And Large Numbers - Index Of Blog Posts