What is dimensional analysis? Have you ever used dimensional analysis in your everyday life? Here is the introductory description which is located on the Wikipedia page for "Dimensional Analysis":
In engineering and science, dimensional analysis is the analysis of the relationships between different physical quantities by identifying their base quantities (such as length, mass, time, and electric charge) and units of measure (such as miles vs. kilometers, or pounds vs. kilograms vs. grams) and tracking these dimensions as calculations or comparisons are performed. Converting from one dimensional unit to another is often somewhat complex. Dimensional analysis, or more specifically the factor-label method, also known as the unit-factor method, is a widely used technique for such conversions using the rules of algebra.[1][2][3]The concept of physical dimension was introduced by Joseph Fourier in 1822.[4] Physical quantities that are of the same kind (also called commensurable) have the same dimension (length, time, mass) and can be directly compared to each other, even if they are originally expressed in differing units of measure (such as inches and meters, or pounds and newtons). If physical quantities have different dimensions (such as length vs. mass), they cannot be expressed in terms of similar units and cannot be compared in quantity (also called incommensurable). For example, asking whether a kilogram is greater than, equal to, or less than an hour is meaningless.Any physically meaningful equation (and likewise any inequality and inequation) will have the same dimensions on its left and right sides, a property known as dimensional homogeneity. Checking for dimensional homogeneity is a common application of dimensional analysis, serving as a plausibility check on derived equations and computations. It also serves as a guide and constraint in deriving equations that may describe a physical system in the absence of a more rigorous derivation.
Wow! Does that sound complicated? Basically, what the description says above is that if you are comparing the mass of two oranges, both the units of measurement (weight) in this case have to be in the same 'units' - grams, pounds, kilograms, etc. If you weight orange number #1 and report a weight of 70 grams, then try to compare a second orange's weight reported as 0.400 kg (kilograms) - then the comparison cannot be completed.
At least until you convert the weight of orange #1 to units of kilograms or weight #2 to units of grams. If both weights were expressed in the same units -- say grams, then orange #1 weighing = 70 grams -- would be much smaller than orange #1 weighing = 400 grams. The same logic applies to base quantities (dimensions) -- like length, mass, volume, height, speed, etc.
How about trying another route to clarify the description in the excerpt above. If you have ever tried to follow a recipe while cooking, then chances are you have engaged in 'dimensional analysis' without knowing that you were doing so. Don't believe me? Follow the quick cooking example below.
Example: Cooking
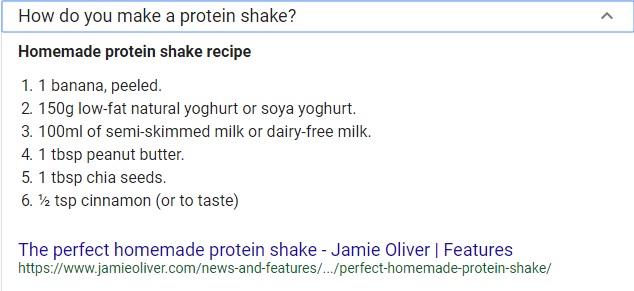
Here is a quick example of using 'dimensional analysis' in your kitchen. Take the recipe shown below as an example:
The recipe above calls for 100 mL of milk. That is 100 milliliters of milk. What if the kitchen in which you are preparing the shake does not contain a 'measuring cup' shown below which is extremely useful in converting between different units of measurement:
|
|
| Source: HomeDepot |
Upon closer inspection of the image of a 'measuring cup' above, one can easily see a series of markings at different heights with different labels. These labels indicate different volumes of measurement in different units. According to the image of the recipe shown earlier, the amount of milk called for in creating the shake was 100 mL -- Which could easily be converted using the instrument above -- i.e. measuring cup.
Although, what would you do if you did not have a measuring cup within the kitchen in which preparation of the shake was taking place? How would a person find the conversion factor to convert between units of 'milliliters' and units of 'cups'? One easy method with the advent of the internet has been to resort to to a 'search engine' like 'Google' or 'Bing'.
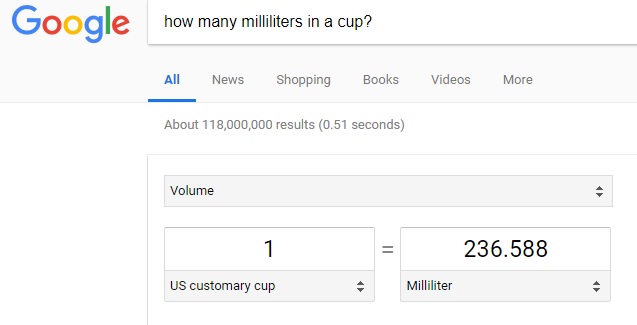
Proceed to bring up a web browser and bring up Google.com and type in the search space: "How Many Milliliters In A Cup?" and the web page with the conversion (interactive) columns should appear as shown below:
Note: The conversion shown above is 'interactive' - which means that the labels are 'drop down' menus which can serve to change either 'units of measurement' or 'dimensions' (i.e. length, area, volume, time, speed, etc.). Feel free to play with the web page to convert between units of various dimensions.
Next, with the conversion factor known which will assist us in converting between units of 'cups' and units of 'milliliters', the remaining step in the conversion is to carryout a mathematical operation as shown below:
The result indicates that in order to follow the recipe (approximately -- not precisely), roughly 1/2 cup of milk will correspond to 100 milliliters of milk. Note that the conversion is approximate -- since 1/2 = 0.5 not 1/2 = 0.423 !!!
Is the method of carrying out a dimensional analysis problem is clear? If the answer is yes, then you are ready to read past blog posts which mainly use 'dimensional analysis' to cast statistics reported in the news into perspective -- click here to access the index of past blog posts. If you are not comfortable with carrying out 'dimensional analysis' problems, see the tutorial below.
Dimensional Analysis Tutorial
A Tutorial on Dimensional Analysis is shown below:
After watching the video above along with reading the content of the blog post so far, you may be wondering where to get conversion values if not from the internet. Science textbooks have conversion tables. After a quick search of conversion tables, the 'Accidental Scientist' appeared with a host of information. Here is a screenshot of an example of a table of conversions below. Note: if you click on the source, you will be directed to the site:
As you can see, there is no need to memorize conversions -- at least all of the conversions. That is what reference materials are for when needed.
Conclusion...
In the paragraphs above, the useful (and fun) method of carrying out calculations using 'dimensional analysis' was shown. Armed with the power to carry out comparisons with conversion factors allows you to verify a large portion of statistics which are reported in the popular news on a day-to-day basis. Is this useful? Depends on how much energy that you choose to exert in understanding the process of using it to live a better life.
Understanding the power of comparison with conversion factors will add extra dimensions of happiness to your life. How do I know? When a person can visualize or comprehend the magnitude of a reported statistic by putting the value into perspective using dimensional analysis, the problem or subject matter of the news article becomes that much more useful to the reader. Again, thank you for visiting the website and check out the dimensional analysis blog posts by clicking here.
Related Blog Index:
Dimensional Analysis Of Statistics And Large Numbers - Index Of Blog Posts


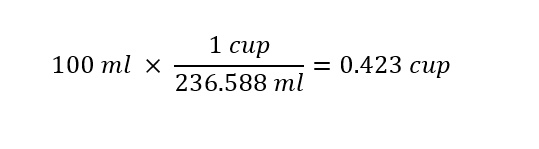

No comments:
Post a Comment