Volume Of Rain Flowing Down The LA River
I start with the question: How much rain is flowing down the LA river? The reason why I chose this question in particular was due to a couple of recent news items sent to me electronically by friends. First, a friend posted a video on Facebook shown below:
Below the video in the notes the following message appeared regarding the video:
Is the California drought a scam?
"An inch of rainfall in L.A. generates 3.8 billion gallons of runoff, so you're talking about more than 12 billion gallons of water that could be captured, but that flows within hours down our concrete streets and into the ocean. There’s enough rainwater to be harvested to produce 30-50% of the entire city’s water needs."
"About half of the rainfall flowing down the Los Angeles River in a typical storm is lost to the ocean, according to the Water Augmentation Study from the Council for Watershed Health, a L.A.-based environmental organization. Most of the rainwater that bounces off roofs, parking lots, streets and sidewalks ends up in storm channels that flush rainwater into the ocean. That amounts to 10 billion gallons from an average rainstorm, enough to fill 120 Rose Bowls, said Alix Hobbs, president of Heal The Bay."
I have to admit, the video is not exactly the same video that I saw on Facebook. Still, the video appears to be very similar and to drive home the point of water just flowing out to sea. The posts on Facebook are labeled with concerns about 'wasted water.' Of course, the problem here is that the water is dirty and would need to be treated downstream and purified to be of any use to residents. With the exception of watering crops possibly (maybe).
The point is: the video above shows a massive amount of water due to just a couple of inches of rain fall. A statistic of 10 billion gallons is reported by the author above. Is this really correct? Can that much rain be falling from the sky and equate to a couple of inches of rain?
In a recent Los Angeles Times article titled "El Nino Rains Get LA Rivers Roaring To Life" the author reports an extremely large magnitude of volume of rain that is attributed to the El Nino storm. A video is attached to the article showing the flow of water down the LA River. I would recommend watching the 30 second video before continuing to read. The reported large volume is reported as a function of flow rate:
The river at its peak can move 146,000 cubic feet of water every second. At its normal rate, the Colorado River, sculptor of the Grand Canyon, doesn't do a quarter of that.
In the future, I will understand why reporters love to cite volumes in 'cubic feet.' For now, we just need to understand how many gallons/second is that equivalent to? The first calculation that I will perform (or show) will be the conversion of the 'flow rate' of 'cubic feet/second' to 'gallons/second.' I can think more clearly using units of 'gallons' rather than cubic feet. Below is the conversion:
Next, I asked myself, how long at the flow rate would the river have to flow in order to equal 10 billion gallons. Here is the calculation below:
Just over 2.5 hours -- Wow!!! That fits nicely with the values reported in the video notes. Meaning, that if water is flowing down the LA River, accumulating 10 billion gallons is not inconceivable. Not in the least. Of course, the flow rate used for the calculations is based on the 'maximum' speed recorded of the LA River in history. Regardless, the important message is that given enough time, a large amount of water flows down the river -- which would call into question the need to scare the public about droughts in California. I realize that the water is not usable directly from the river.
You might be wondering why I am thinking about the subject. I mean, aside from the recent storms that have hit Southern California over the past week and a half along with the blaring news bites about 'El Nino'. Part of the answer lies in the fact that I had large amounts of water on my mind when writing the earlier post regarding the flood in Brazil as a result of a damaged dam due to mine waste water. The other part is due to news which I received over the winter break visiting family.
How Many Gallons Of Water Equals 2 inches Of Rain?
Over winter break, we got together with family. Getting together means talking about current events. One current event was the rainfall that was hitting the Lake Tahoe region. The reason being is that my brother-in-law's family lives up near the lake. Each year, my sister and her family go and tear up the ski slopes for a few days. Therefore, their interested in storm reporting in the region.
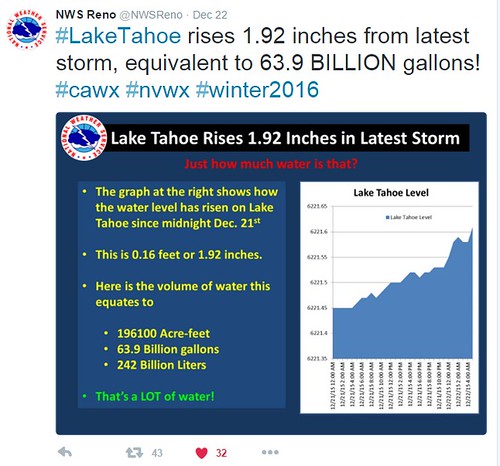
Anyways, during a conversation regarding the weather up in the region (Lake Tahoe), I heard a number which blew my mind. I almost thought that I had a hearing issue. I asked for clarification and sure enough, I had heard correctly. The number in question was the amount (volume) of water that filled up 1.92 inches in Lake Tahoe was equivalent to 63 billion gallons.
At first, I did not believe this number to be correct. In fact, had I not previously been entertaining the number (15.9 billion gallons) which was equivalent to the mining spill in Brazil, I really would have thought my family to be insane.
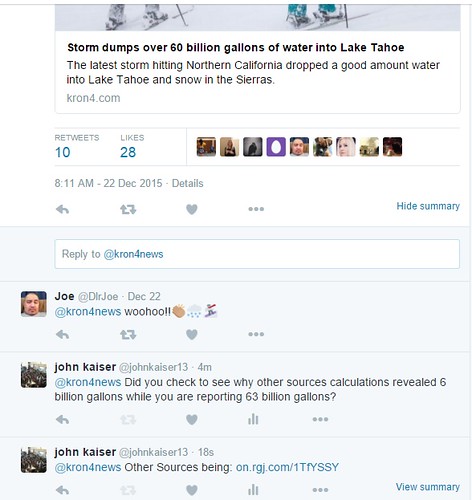
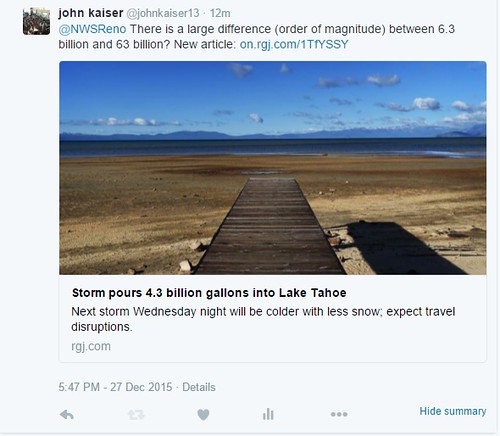
When I got home, I immediately looked up the number. Sure enough, according to the news site 'KRON,' a heavy storm dumped enough rain to add 60 billion gallons of water into Lake Tahoe. Here is a 'tweet' that I found on the new sites Twitter account shown below:
After finding the tweet shown above, I just still could not wrap my head around the gigantic volume of 60 billion gallons correlating to just 1.92 inches of rain. I would believe more height to be associated with that volume. Why did the volume bother me terribly? I guess because I had not yet checked the number with a calculation of my own.
First, I think a little perspective might be needed at the moment to visualize this massive amount of water. If you have never visited Lake Tahoe, then the volume of water contained in the lake is truly unimaginable. The shoreline perimeter is 72 miles around the entire lake. One can even see the lake from space.
With the information about the LA River along with the image above, the volume reported does not seem outlandish. Although, at the time that the number of 60 billion gallons was reported to me, all of the above information had not been known to me. I had to do a small amount of research -- which is part of this post.
In fact, when we (you and I) hear or see statistics, we should not just take them at face value and believe them. A small amount of research can go a long way -- as you will see shortly. Without knowing much, how could a person check to see if the number was correct?
How can the volume be determined knowing the value of both perimeter and height?
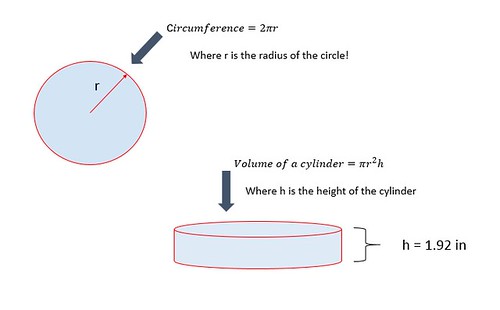
Well, knowing the value of the perimeter in miles allows us to carry out an approximation to determine the volume. We could approximate the lake to be a circle and then figure out the volume based on an equation for a cylinder. Below, I show the approximation I made initially to do a 'rough check' of the reported number.
In the picture above, a circle is shown with a 'circumference' (as "C" equal to 72 miles -- perimeter of Lake Taho) which is equal to a factor of 2pi multiplied by a 'radius'. Since the 'circumference' is known, the 'radius' can be determined through rearranging the equation -- as shown below.
The calculated radius is expressed in units of 'miles'. In order to calculate a volume of a cylinder with height expressed in units of 'inches' then the radius must be converted from 'miles' to 'inches' as shown below:
With the radius known, the next step toward figuring out the volume of rain that correlates to the 1.92 inches of rain that was deposited into Lake Tahoe is to use the equation for the volume of a cylinder. In the same picture with the circle, there is an equation for the volume of a cylinder. A factor of pi squared multiplied by the radius and height gives the total volume of a cylinder as shown below:
The volume is expressed in 'units' of cubic inches -- which might not be useful for most people. Unless, of course, you think in terms of cubic inches or cubic feet, etc. To each his own! I am more comfortable with gallons and since the article cites water volumes in gallons -- we will stick with that unit. Therefore, below the equation for the volume, I converted the volume expressed in units of cubic inches to units of gallons using dimensional analysis.
According to my approximation using a circle, the answer (for volume) is short compared to the value reported by the news (KRON) of 63 billion gallons. Why? Ask the following questions:
1) Is the 'run-off' water from surrounding region (the mountains) the difference in volume?
2) Is the approximation of a circle that far off?
3) Is there a more accurate way to calculate the volume?
I had these questions after calculating the differences in volume. One of the most powerful advantages of having access to 'social media' is the ability to ask questions. I decided to inquire into the difference between the number I calculated and the reported number. In order to inquire into the difference, I had to find out where the number (reported number) originated.
-Transparency in reported numbers is needed
I started looking into the origination of the reported number of 63 billion gallons of water that was supposedly dumped into Lake Tahoe. What I found was very interesting. You might find the answer to be drawn out, but that is how research is done on a everyday basis. Why should investigating the source of a 'reported value' be any different? The methodology is the same as shown below.
First, I found an interesting article upon investigating further the source of the volume of 63 billion gallons of water which differed from the original value. The 'SF Gate' reported a number far less than either the original value (63 billion gallons) or our calculated value (14 billion gallons). Their value was based on a 'correction' of 6.3 billion gallons. Wow! The difference being nearly 57 billion gallons from the original value and half of our calculated value (14 billion). What is going on here?
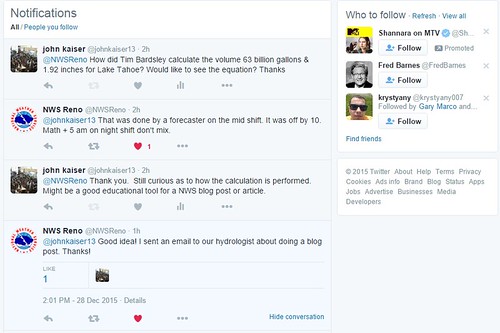
I decided to turn to social media (Twitter) and ask KRON about the difference in values as shown below:
Shown above is the inquiry to which I have yet to receive an answer from KRON for. I decided to find out where the news organizations got the source from. After searching into the twitter accounts of both KRON and SFGate, I found that the source originated from the National Weather Service -- Reno office. Finally, I found the source on their Twitter feed shown below:
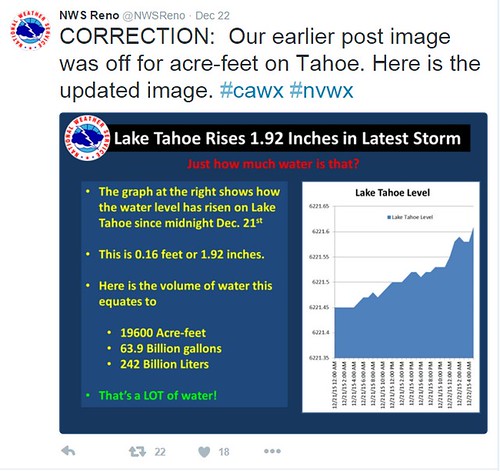
Above the tweet is another correction to the original reported value shown below:
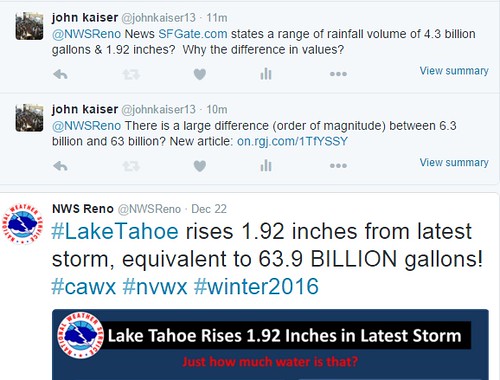
The correction was to the value reported in "Acre-feet". I wondered if another correction would be issued for the value reported in 'gallons.' I decided to ask the NWS Reno by tweeting to them as shown below:
I included the article reporting the difference in volume -- which was significant -- below:
I waited for an answer and expected one. Not really. Although, a few news agencies are good at getting back to an inquirer quite quickly. Therefore, if you have a question, go ahead an ask someone via 'social media'. You might be surprised at the ability to get a question answered. Since the question above was to a government agency, my expectation was low.
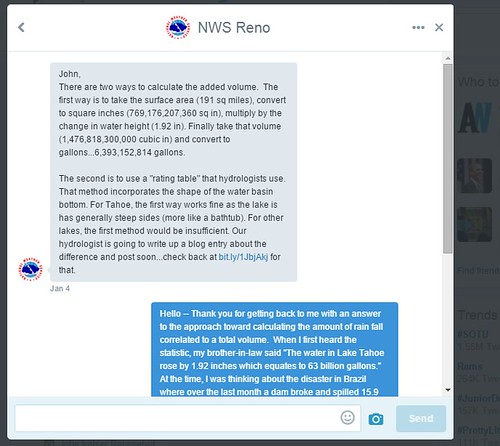
A few days later, I was pleasantly surprised when an employee from the National Weather Service at Reno responded to my question on Twitter. Shown below is the response:
The forecaster that performed the calculation was Tim Beardsley from the NWS Reno. As indicated above, the initial value that was calculated was off by a factor of 10. Meaning, that the true number was 6.3 billion gallons of water NOT 63 billion gallons of water. Additionally, you can see that I still asked to see the equation or method that Tim used to calculate the value. I was left still unsatisfied.
Surely, I should be able to calculate the value to within the same 'order of magnitude'. At this point in time, I had to wait for another response. Keep in mind, this correspondence was occurring over the holidays. I was surprised that any responses were given. The first week in January, Tim Beardsley responded with the method that he used to calculate the volume of water into Lake Tahoe corresponding to 1.92 inches of rain fall. Shown below is his response on twitter:
After reading his response, I could see that his method was simpler. I did not realize that a value for the surface of Lake Tahoe was known. I felt rather stupid -- brain fart. Of course, use the area of the lake and then multiply that value by the height -- as shown above in the equation for the volume of a cylinder.
To verify his calculation, I repeated exactly what was reported above in the tween response. I show the results below:
As you can see, the calculation is easier than our approach. The calculation is simplified by having the 'area' -- which is equal to (pi multiplied by the radius squared).
Still, the question remains where the difference of almost double the volume comes in. I imagine that the difference is due to the calculation of the perimeter distance. Or that Lake Tahoe is not a perfect circle.
Conclusion
Regardless of the true value reported here by the news organizations, a few observations can be made in conclusion:
1) Do not take a value reported by the news as to be 'absolute truth'.
2) Different methodologies of calculating volume can give VERY different answers.
3) Different answers have VERY different meanings.
Again, no one is perfect as shown above. There were two considerations that were not discussed in the blog post among others (I am always open to suggestions). The first was that in the corrected twitter post by the NWS Reno, the value of 'acre-feet' was off by an order of magnitude. A large difference exists between 196,100 acre-feet and 19,600 acre-feet. How large? Exactly 176,500 acre-feet. How did that difference arise during the calculation?
The second consideration was that there exist a second method by which to calculate the total volume of rain fall by hydrologists. According to the explanation above from the NWS Reno, a 'Rating Table' is used by hydrologists (click here). Regardless, a greater degree should be a goal of the National Weather Service in Reno regarding the method of calculating weather conditions.
A few readers might not agree with the last statement regarding organizations being more transparent with their methodologies. Ask yourself the following question:
How many times have you looked out the window after looking at the weather forecast and said "Wow, the weather channel really got that wrong?" "I wonder how the weather channel came to this conclusion?" This should warrant a greater degree of transparency -- for those interested in understanding the methodologies used.
As I have shown above, the amount of rainfall that drops on Southern California is quite large. Not just quite large, but HUGE. Scientists and engineers should be trying to come up with methods to capture this water for alternative methods. Or at least building 'floatable turbines' or another method to turn the mechanical energy (the energy of flow of water) into electrical energy. What do you think? How would you harness that power? Until next time, enjoy pondering the numbers reported in the post. Have a great evening.
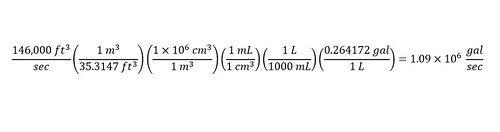



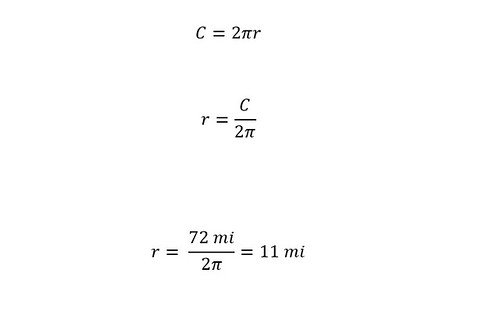

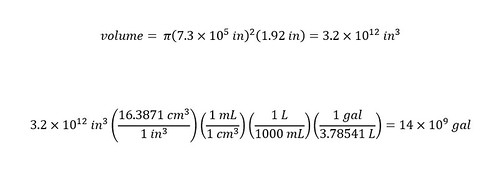

No comments:
Post a Comment