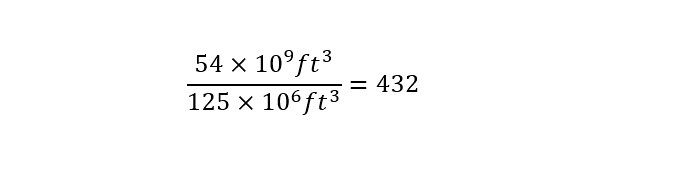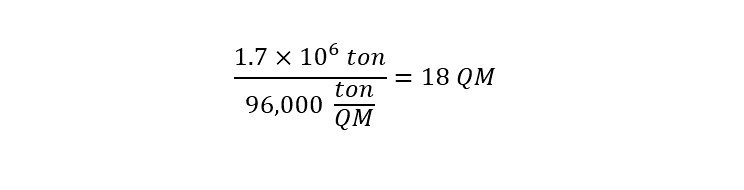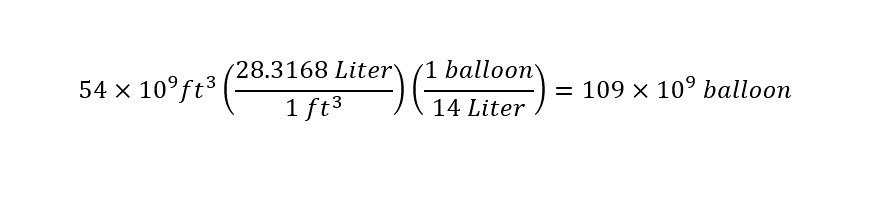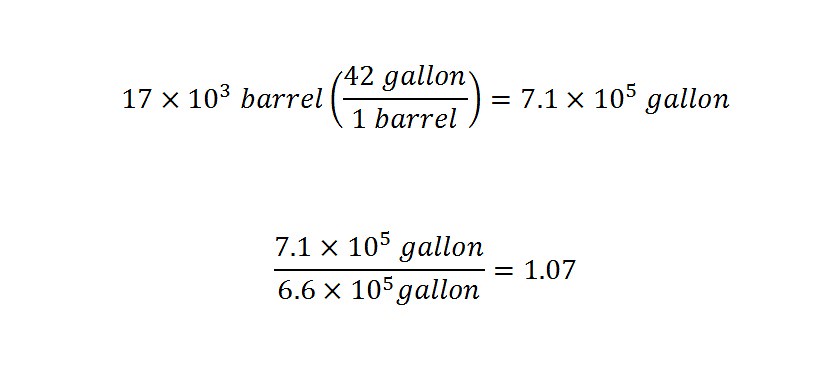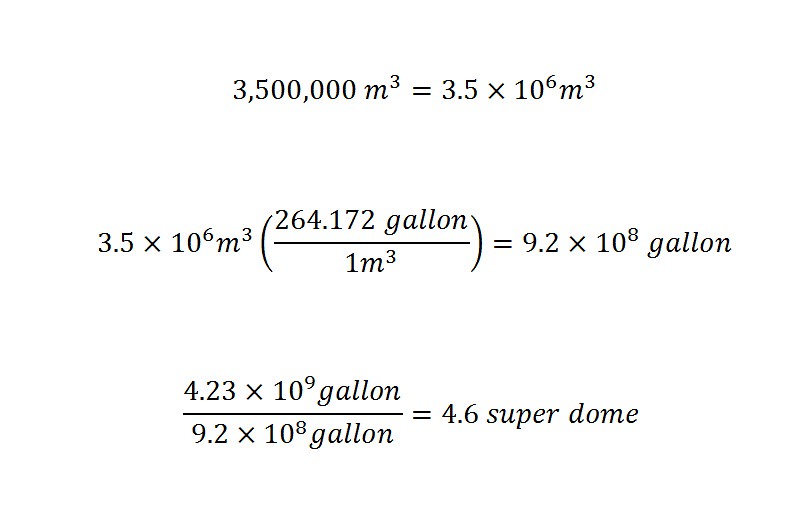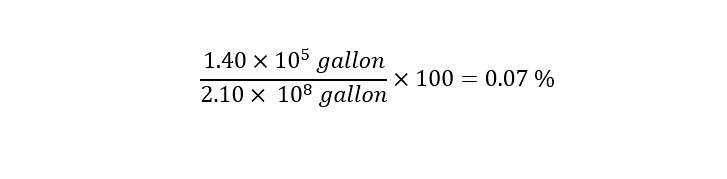How Much Weight Can 54 Billion Cubic Feet Of Helium Lift?

If you were to release a balloon filled with helium outside, what would happen?  The balloon would rise up until the pressure in the atmosphere caused the balloon to burst releasing the helium inside (which would rise until escaping the atmosphere -- the subject of a previous blog).  The blimps that fly high above us are in part operated by helium (lift provided by the gas).  What is the point right?



Recently, a large helium deposit was found off of Tanzania in Africa that holds an estimated 54 billion cubic feet.  WOW!  Thinking of helium from the perspective of providing "lift" in a balloon, how much weight could the amount contained in the reserve (in Africa) lift?  Read on to find out the answer.

How Much Volume Does 54 Billion Cubic Feet Of Helium Occupy?

As readers of this blog site know, one of the many goals is to demystify science along with the large numbers and concepts that come with the field.  Recently, an article titled "Scientists Make Huge Helium Discovery (On Planet Earth)"  appeared on the website "ChemInfo" that unveiled a new helium deposit that has been found in Africa.  Here is an excerpt detailing the new discovery and the importance from the article:

The scientific community has been abuzz for years that the earth is running out of helium. Though it is one of the most abundant resources in the universe, helium is in limited supply on earth. And once it’s extracted and used, it’s gone forever.

Helium is a rare and vital commodity with many uses including industrial leak detection and deep sea diving equipment. Liquid helium is also used as a coolant for rocket fuel and as a superconductor for magnets in MRI machines. Plus, kids love it at parties.

Because our stockpile of helium has been dwindling at the National Helium Reserve in Texas, with no known new helium gas fields to extract it from, concerns have mounted that the days of floaty party balloons could soon be ending. Recently, scientists made a major discovery that could change that.

For the first time, researchers have pinpointed a giant helium gas field. Usually, helium is discovered accidentally when extracting oil and gas. Up until this point, scientists had never intentionally located a helium field. But the discovery was made after a team from the University of Oxford and Durham University collaborated with a Norwegian helium exploration company, Helium One, and set out to see if it could be done.

If you are wondering whether the world is getting desperate for helium, you are correct.  As the world consumes helium through the avenues listed above, including the semiconducting industry (the largest user), reserves are becoming more precious.



This is why researchers are becoming "proactive" in their search as described above.  Just think about the prospect of not being able to get an MRI at the hospital after sustaining an injury -- due to the lack of a magnetic field which is dependent upon metal windings being immersed in a bath of liquid helium.  Once charged, the metal windings hold the current circulating at zero resistance (superconductivity) until the wires become room temperature again (helium boils off).



How much helium was discovered?



Here is another excerpt regarding the discovery amount shown below:

The researchers estimate that the field could be holding as much as 54 billion cubic feet of helium, which is more than twice the amount being currently held in the U.S. If correct, the field could help supply the world’s helium for generations to come.

Assuming the detection methods are accurate, the team says the next step will be finding the best place to extract the gas. They also hope that the discovery could potentially lead to scientists uncovering more helium fields.

Sticking with the past blog posts on this site, how does a person comprehend such a volume of helium?  First, I should point out that the amount is in question due to the measurement device.  That is an important bit of information.  Why?  The amount detected is only as accurate as the measurement device.  Furthermore, just because the amount is assumed to be that large, the actually amount extracted could be different.



How different?



Probably no more than an order of magnitude.



In order to visualize the enormous amount of helium that has recently been discovered in Africa, lets return to an old post.  As you will recall, there was an enormous amount of gas leaked from a storage facility in Southern California -- the Aliso Canyon Gas Storage Facility -- starting the end of last year.  The leak was massive enough that the total amount of gas leaked turned out to be around 5 billion cubic feet leaked.



The underground storage reservoir was estimated to hold around 184 cubic feet of gas.  A reader sent in a comment to correct me and said that the gas was under extreme pressure, therefore, the total space of the reservoir was less (but how much less) -- not too much less.  The fact remains that the amount of helium discovered in Africa is within a range of volume that has been put into perspective.



Specifically, how many Mercedez Benz Super Domes would have to be filled to hold 54 billion cubic feet of helium gas?



In order to carry out the calculation, the volume of the Super Dome needs to be known -- which is around 125 million cubic feet interior volume.  A picture of the exterior of the Super Dome is shown below:

                                              Source: Photo by David Grunfeld (Nola.com)



With the interior volume of the Super Dome known to be 125 million cubic feet, the amount of Super Domes that could be filled is calculated by dividing the two numbers as shown below:

Wow!  The amount of gas that was discovered underground is enough to fill 432 Mercedez Benz SuperDomes?  My goodness, that is a large amount of gas.  I am constantly amazed at the volumes that are listed in these news stories.  Like most readers, I read the same statistic -- 54 billion cubic feet -- of helium and think the following:  That must be an enormous amount?



By performing dimensional analysis, I am one step closer by comparing the amount to other statistics in the news, such as the Porter Ranch Gas Leak I mentioned above.  Dimensional analysis allows me to place the number in a better place -- a place in my mind of perspective.  Store that number next to Porter Ranch under the mental file -- excessive amounts of gas -- really incomprehensible.




The question that was intended to be answered in the blog post was the following:



How much weight can 54 billion cubic feet of gas lift?



This requires us to think like blimp designers.  Lets do some math below to find out.

How Much Weight Can 54 Billion Cubic Feet Of Gas Lift?

To tackle the question of the blog post, we must think like a blimp designer to a small extent.  In theory, a blimp is filled with helium and can provide a large amount of lift to accomplish a task.  The blimp in question could look like the following -- only much larger:

Source: ABC News

Shown above is the 'Goodyear' Blimp.  According to the website 'HowStuffWorks.com,' the average blimp holds a volume of gas in the range of  67,000 -- 250,000 cubic feet of helium.  Since the volume of gas that is contained in the ground in Africa is enormous -- nearly 5 orders of magnitude larger, our imagination will have to suffice.  Just think of the blimp above just many orders of magnitude larger -- use creativity.



In order to calculate the amount of weight that 54 billion cubic feet of gas can lift, a ratio of volume to weight needs to be determined for a balloon.  I found the answer on 'StuffYouShouldKnow.com' in a post titled "How Many Balloons Would It Take to Lift You Off The Ground, Answered" for the amount of balloons required to lift a person off of the ground.  Lets start by learning from 'frames' taken in the video to determine how many balloons are required to lift a person off of the ground.  From there, the volume can be changed to the volume in question and then determine the weight!



Here are the slides with the relevant information to answer the following question:



How many balloons does it take to lift a person off of the ground?



First, the amount of helium needs to be known for a single balloon along with the weight that can be lifted as shown below:

Next, the volume in a typical balloon needs to be known as shown below:

Next, the logic amounts to the following:



1) If 1 Liter of helium can lift 1 gram, then 14 Liters of helium will lift 14 grams.



2) If a person weighs 50 Kg = 110 pounds, then 3500 balloons should lift them off of the ground?



The last statement is shown with no calculations -- which is bothersome if you are the author of this blog site -- right?  In light of this stretch, I calculated the amount of balloons needed to lift 50 Kg as shown below using the video producers logic:

Therefore, 50,000 grams of weight will require 50,000 Liters of helium.  If each balloon holds 14 Liters, then dividing 50,000 Liters by 14 Liters will yield the number of balloons.  In this case, the number calculated revealed just over 3500 balloons would be needed.  The number coincided with the number stated in the video above.



Therefore, I felt comfortable with the ability to reproduce the number reported in the video with the values (parameter values) listed in the video.  This is important for reproducing results.  Reproducing results is increasingly important in science today more than ever with the exponentially growing number of studies being published hourly.



Next, using the values in the video -- I calculated the weight (number of tons).

Wow.  As expected, that is a large amount of weight that can be lifted by 54 billion cubic feet of helium.  How can that number be put into perspective?  In a previous post, the weights of two large objects (Airplane: Spruce Goose and Ship: Queen Mary) were compared and contrasted.



How about using  the weight of the Queen Mary -- which was 96,000-tons?



How many Queen Mary Ships can 54 billion cubic feet of helium lift?



Before the calculation are shown, a picture of the Queen Mary ship might assist you in putting the enormous weight into perspective.   Here is a picture of the Queen Mary below taken from 'Wikipedia':

Source: By RMS_Queen_Mary_Long_Beach_January_2011 -- David Jones 

The calculation is shown below:

According to the calculation, 54 billion cubic feet of helium contained in a 'Goodyear Blimp' could lift the equivalent weight to 18 Queen Mary ships.  WOW.  That is a large amount of helium.  I guess now I understand the enormous enthusiasm behind the discovery off of the tip of Africa.



Just for fun, I thought that I would calculate the number of balloons that could be filled (for celebrations: birthday parties, anniversaries, graduations, etc.).  I show the calculation of the number of balloons that could be filled with 54 billion cubic feet of helium below:

That is an incomprehensible number -- 109 billion balloons.  That would be an enormous number of celebrations.  More than during the span of our lifetime.



Have I made the point yet?



What point?

Conclusion

The discovery of an underground reserve of helium off of Africa has the potential to supply the world with helium for a few decades.  This is reassuring, especially, since just a couple of years ago, the government started discussing the possibility of "rationing" helium to the world.  The current discover is a relief to say the least.  How big is the discovery?  I hope that I have put the enormous number into perspective for you in the paragraphs above.




In a future post, I will explain further why the discovery is important to the field of science.  I now have a few more useful statistics to compare large numbers too -- and so do you.  The next time that someone asks you how to visualize 54 billion cubic feet of a gas (such as helium), you will be able to quickly answer them with the handy statistics:


1) The equivalent of 432 Mercedez Benz SuperDomes!!!


2) If the volume was contained in a blimp, the blimp could lift 18 Queen Mary ships!!!


3) If the volume was in party balloons, 109 billion balloons could be filled for celebrations!!!



Until next time, have a great day!

Is 94 Million Barrels Of Oil A Large Amount? That Is The Global Daily Demand!

Climate change is an ongoing debate that attracts news often due to the changing weather on the planet.  We (the world) share the atmosphere.  Therefore, all participants should be concerned when we see dramatic examples.  What are these dramatic examples?  China has an atmosphere that is opaque as shown in the picture below:

The take home point is that the issue of climate change is starting to permeate through various circles (board rooms) of various large corporations.  One such corporation is Exxon Mobil Corportation.  Recently, there have been questions generated at the top of the corporate structure about the direction of the future.  Where do we stand?  The global oil demand is 94 million barrels (by one estimate) every single day.  WOW!  How do we visualize that large of volume?  Below are a couple of ways that might be helpful.

Investors Push Board Of Exxon For Answers!

In a recent artile from the New York Times titled "Exxon Investors Seek Assurance As Climate Shifts, Along With Attitudes," the authors discuss the new emerging trend of investors starting to inquire into mitigating risks associated with climate change.  Here is the new revelation of investors which is indicative of a changing energy landscape:

At the company’s planned annual meeting on Wednesday in Dallas, shareholders will vote on a resolution to prod Exxon Mobil to disclose the risks of climate change to its business.

Such resolutions have been floated before, and they typically do not pass. But there is a growing chorus of investors, many of them large institutional shareholders, who say they are worried that Exxon Mobil, the largest publicly traded energy company in the world, is not adequately preparing for tighter times if countries start acting on the pledges they made last December as part of the Paris climate change accord.

Exxon Mobil, for example, projects that global demand for oil will keep growing — by just over 13 percent from today, to 109 million barrels of oil a day by 2040.

But the International Energy Agency’s projections include one situation where demand could drop by 22 percent, to 74 million barrels a day by 2040, if measures are put in place to keep global warming at levels that, while still dangerous, could avoid the most devastating consequences.

The shareholder resolution calls for Exxon Mobil to publish an annual assessment of impacts of various climate change policies, including ones that would lead to the steep drops foreseen in the most severe energy agency’s forecast. Another resolution calls for the company to give shareholders a bigger say over governance.

The excerpt above highlights the major issues that society faces in today's fast-paced changing world.  I think that the authors did a great job of summing the issue up.  The impact of the Paris Climate Talks is gaining momentum by the fact that the subject is making news.  I was amazed to see that the results of the climate talks last December is actually causing a downstream change which is exerting pressure back up the chain.




To have other corporations start to divest stock in companies that are geared toward future renewable energy technology is a main stay in the current popular media.  Further, to have a story about consumers starting to question the practices of these large corporations occupies the same space as a change in technology.  But to have the investors of a large corporation like Exxon Mobil start to ask questions of the Board is a whole new parameter change in the equation toward moving to renewable energy technology.




The investors are serious players in a company -- for if the investor (who holds a large amount of shares) gets scared, then he/she can dump their stock and cause problems for the corporations.  Here is a question in the form of an excerpt that sums up the issue from the article shown below:

But big owners of the stock worry that the optimism of Exxon Mobil’s outlook for oil demand is dangerously misguided.

“Investors can’t afford to have Exxon become the next Kodak,” said Scott M. Stringer, the comptroller of New York City, whose pension fund owns roughly $1 billion worth of Exxon Mobil stock.

“It is impossible for them to do business for the next 100 years as they have the last 100 years,” added Mr. Stringer, who supports the risk-disclosure resolution

This is a wake-up call for these large corporations.  But, what really caught my eye were the numbers representing the increase or decrease in daily global demand in oil.  Upon first pass (reading), I was trying to figure out what the exact daily global demand is -- really a ball park figure?  I am sure that the process of trying to get the numbers to estimate the total number of barrels in oil on a daily basis is complicated.  I decided to type into google a question -- shown below:

As you can see, the first boxed statement indicates that the daily global demand is around 94 million barrels a day.  Oh my goodness.  WOW.  If you look down the list, there are two other sources that I inlcuded in the picture.  I read both to make sure that the first figure was on par with the range that was mentioned in the New York Times article above.





Another statement that caught my attention was on the website "Watchdog.org" listed as the 3rd entry above.  Here is an interesting and eye-catching statement guiding the reader to put the huge global daily demand of oil into perspective.  The author uses dimensional analysis with no equations but with dimensions that have been used on this blog site before -- the Olympic Size Swimming Pool.  Here is the excerpt:

“It’s mind-boggling,” Peter Tertzakian, the chief economist and managing director of Canada’s ARC Financial Corporation told participants at the Platts North American Crude Oil Summit last Thursday.

To put that number in perspective, Tertzakian offered this nugget: “That’s the equivalent of draining an Olympic-size swimming pool every 15 seconds.”

“You can say, pardon the pun, the world goes ’round on oil,” Tertzakian told Watchdog.org.

Previously on this blog site, I have used the Olympic Size Swimming Pool to put a large volume of water into perspective.  You will recall here on the introductory post!   In that post, the calculation involved determining the amount of Olympic Sized Pools that would be filled with 20 million gallons of oil -- which was spilled in the Exxon Valdez Oil Spill in 1987.  Kind of ironic with the subject matter in the current post -- right?  The calculation revealed the spill would fill 30 Olympic Swimming Pools.  I thought that volume was large.  Keep on reading.

How Many Olympic Size Pools Could Be Filled?

In the article, the author included a picture of an Olympic Size Swimming Pool to drive home the result of dimensional analysis.  Here is a picture of an Olympic Swimming Pool from "Wikipedia":

Source: Wikipedia

Without further ado, the volume has been stated in the excerpt above of 94 million barrels of oil per day -- represents the daily demand for the world.  Further, in the article from "Watchdog.org" the statement says that the volume corresponds to an Olympic Size Swimming Pool being filled every 15 seconds.  Is that correct?  How does a person check this fact out through dimensional analysis?





First, the amount of water that occupies the typical Olympic Size Swimming Pool needs to be known.  Taken from "Wikipedia" the amount if 660,000 gallons.  Additionally, the conversion of barrels to gallons needs to be known too.  First, I calculate the amount of barrels in 15 seconds as shown below:

The amount of barrels delivered in 15 seconds is 17,000-barrels.  How many gallons are in a barrel of oil?  The news typically reports volumes of oil in barrels rather than gallons or liters.  Shown below is the image of typing the question of conversion units from google:

The image above is helpful or should be to the reader.  Not all conversion factors have to be taken from a reference book or a text book.  To lower the barrier toward carrying out the calculation, just ask google.  With the conversion, the amount of gallons in 15 seconds can be determined as shown below:

There are 710,000-gallons in 17,000-barrels of oil.  Additionally, I took the liberty to complete the calculation of comparing the amount of barrels to the volume of an Olympic Sized Swimming Pool.  Basically, the statistic cited in the "Watchdog.org" article was correct.  Nice, I like when the media do their calculations correctly.




Is there any other dimension or volume that could be chosen to further put the volume in perspective?




How about the world's largest swimming pool?




Located in Chile, the world's largest swimming pool is 66,000,000-gallons.  WOW.  Here is a photo taken from the "Wikipedia" site:

Source: Wikipedia

I wondered how many of these would be filled up by the total daily volume for the global demand -- 94 million barrels.  Here is the calculation below:

64 pools -- how is that possible to put into perspective?  My mind was bent.  I like large numbers and see them a lot in science, but this number is incomprehensible.  As usual, I like to look for a variety of volumes to compare the numbers.




How about the Mercedez Benz Super Dome?

How Many Super Domes?

In order to figure this out, I needed the volume of the interior space of the Mercedez Benz Super Dome in Louisiana.  The volume is 3,500,000 cubic meters -- interior space.

Source: Wikipedia

How does a person calculate the volume and compare the result to 94 million barrels?




To start with, the proper conversions need to be carried out;  Specifically,

The next time that you (the reader) are inside the Super Dome think about the fact that 4.5 of these could hold the daily global demand of oil.  Absolutely amazing to say the least.




Have I given you a good perspective of the global daily demand of oil -- 94 million barrels of oil?

Conclusion ...

The next time that you find yourself at the gas pump think about the complexity associated with computing the daily demand of oil globally.  Undertaking this task would require compiling a bunch of statistics from a variety of organizations.  More importantly, I would ask the reader to consider the opposition on behalf of those civilian's who would like to transition immediately toward renewable energy.  Can the world accomplish this task quickly?  What if all of the major corporations decided to make a transition -- how long would that take?  Probably longer than you could imagine.




Yes, I am speculating on this.  Although, upon viewing the perspective given above through dimensional analysis, what is an appropriate time line?  How do we accomplish this?  These are open ended questions which need to be entertained.  You might be wondering at this point:




What can I do to reduce my consumption of oil and contrabution to the global daily demand?




Imagine if each of us cut our usage by just a little.  That would add up to a large number.  Lets all do our part and move toward using/demanding renewable energy technology.




Related Blog Posts:


Dimensional Analysis Of Statistics And Large Numbers - Index Of Blog Posts


Science Topics, Thoughts, and Parameters Regarding Science, Politics, And The Environment!

A California Dream Spoiled By Big Oil

My wife tells the story often to strangers of her evolutional history of becoming a resident of California.  The story usually starts off with a brief introduction to her bedroom as a teenage girl with a poster of the California coastline -- the beach on it.  Dreaming, she says of the following: basking in the sun, meeting her husband, and living near the beach.  In a sense, she has obtained each.  I am a native Southern California guy.  We live inland around 40 minutes drive (without traffic) from the beach.  Periodically, we find ourselves at the beach -- like we did yesterday.  What is the issue you might ask?  Let me explain below.

The California Dream?

As I mentioned, I am a native of Southern California.  I grew up in Corona (California) which is inland from the beach aroun 60 miles.  Corona during that time was a small city.  My parents both grew up in Santa Monica by the beach.  As a result of the tremendous growth, they decided to move inland away from all of the commotion.  Of course, their family still stayed in the area, so the opportunity to visit was always present.




Corona was not the beach.  Although, Corona (during that time) had special attributes of its own.  Originally, Corona was a citrus station filled with orange trees, the urban sprawl was large.  As a result, as children we would ride our bicycles all around town distances 5 or more miles in a single direction.  In hindsight, this training turned out to be useful in motivating our  nonprofit organization -- bikecar101.




Over the years, my siblings and I spent a considerable time at our grandparents house near the beach.  We would go to the beach very often and run around burning off all the excess energy which had been built up throughout the day with other activities.  Surfing was included in the beach trips.  For us, living in California meant both the beach dream and the small town feel which is much different than living in downtown Los Angeles.  Although, today, the city of Corona has grown considerably and has but only a few orange trees left.  The rest is growth (housing and commercial buildings).




Why am I carrying on like this?  What is the point to all of this rambling?




The reason why I discuss my background is to set the stage for the following observation which I am told quite frequently.  My wife, who is from Omaha (Nebraska) will often tell me that I do not appreciate California.  At first this was strange.  I had been to quite a few other countries while serving in the US Air Force -- but that is another story for another time.  Over time, I came to ignore her when she said this to other people.  California is a wonderful place, but just like every other place in this great nation, there are wonderful attributes and not so wonderful attributes associated with the State.




More specifically, within Southern California are the same distinctions.  I am constantly amazed by this observation.  People are interesting and amusing (myself included).  Alright, now that we have that out of the way, lets get down to business.  The "California Dream" was ruined yesterday for me -- sounds strange right?  Is that even possible?  I believe that the possibility exists, let me explain.




Last weekend, a mutual friend of ours wanted to surf at Venice Beach on Saturday.  I have not surfed for a couple of years and had no board, therefore, I was not super motivated to go with him.  I did want to visit and he wanted to surf with a passion.  Turns out he just bought a board rack for his bicycle and wanted to ride down with us and hang out and surf a little.  No problem.




We got to the beach and had a great lunch.  After, he rented a wet suit and we settled on the beach near the water to watch him hit the waves.  To my amazement, the following observations were made by us on the beach that day:




Observation #1: Stain on wet suit




The first observation was a strange smeared stain that was black that ran across the wet suit that Bryce rented.  He really wanted to surf.  So much so that he was willing to wear a wet suit that had a stain which appeared like the suit had been used as "toilet paper" in the rest room.  I am not joking.  Very strange I thought to say the least.




He set out and paddled around for a while until he was tired and returned only to want to immediately get out of that wet suit.  The suit smelled dirty and as a result made him disgusted.  I thought -- after surfing for years -- that is what you get when you rent a wet suit.  At least the water washed the suit off as he was using the suit.   So I thought ...




Observation #2: Mysterious black sticky compound on my feet



When we were leaving the beach, I decided to wash my feet before putting on my shoes to bicycle back home.  I noticed that there was a black sticky compound on my feet that had sand stuck adhered to the patch.  I thought at first that upon walking across the grass near the beach, I might have walked through a patch of "dog poop."   Nope.




When we arrived at the showers, I tried to wash the stuff off of my foot.  To no avail, whatever was adhered to my foot was there to stay.  Kayla even tried to wash is off and smelled the substance to identify the smell as "bong resin."  Bong resin is the tar that accumulates at the bottom of the pipe used to smoke marijuana and stinks while having the property of being "super sticky."  I thought that the possibility of that substance stuck to my foot being "bong resin" was strong since the smell of marijuana is all encompassing Venice Beach.  I decided to stick my sock on and ride home to deal with the sticky substance stuck to my foot after in the shower.




Observation #3: Sticky substance was not "bong resin"




To my astonishment in the shower, the substance was definitely not "bong resin."  How do I know?  There was no smell or trace odor of marijuana upon closer inspection.  What was this substance?  Turns out later while talking with some friends over dinner that night who surf down at Venice, the substance was "tar."  Basically, the tar had been more common place since the oil spill by the company -- Plains All American Pipeline -- up the coast last year in Santa Barbara.  What?  That was "oil tar."

Oil Spills Aftermaths Linger For Years

I remember reading the in depth coverage of the oil spill in Santa Barbara caused by the Plain Oil Company which resulted in around 140,000 gallons of oil dumped onto the coast.  My first thought was to compare that amount to the gigantic oil spill in the Gulf of Mexico by the BP Oil company years ago.  Here is a direct calculation of the ratio of the spills:

Yes, the number is super small in comparison.  For this reason, I did not think to much of this spill.  In the initial blog post of this website (introductory blog post), I calculated the number of Olympic sized swimming pools that would be filled with the equivalent volume of the Exxon Valdez Oil Spill in 1989.  This turned out to be 30 Olympic sized swimming pools -- Wow.  What about the oil spill in Santa Barbara of 140,000 gallons of oil.  Shown below is the calculation:

Compared to other oil spills, the Refugio oil spill in Santa Barbara did not seem that large.  I would have thought that over the course of a few months, the oil would have dispersed enough to be "non-existent" -- or removed from the local beaches.




Of course, any spill can be catastrophic -- regardless of volume.  According to the news accounts, the damage to the environment was not known at the time and would take a while to tally.  There was a large difference between the oil spills that I should mention before proceeding.  The Refugio Oil spill that occurred in Santa Barbara (California) was very close to the coastal beach.  Whereas the gigantic oil spill off the Gulf Coast of Mexico was a distance offshore.  This point of distinction needs to be made before proceeding further.  Regardless, according to the news accounts, the damage was serious.




According to a news story released nearly 10 days after the spill that appeared on the website "The Guardian" titled "Globs Of Tar Was Ashore, Closing Los Angeles Beaches," the beach was not inhabitable by visitors.  Here is an excerpt from the article:

Popular beaches along nearly seven miles (11 kilometres) of Los Angeles-area coastline were off-limits to surfing and swimming on Thursday as scientists looked for the source of globs of tar that washed ashore.

The sand and surf on south Santa Monica bay appeared virtually free of oil after an overnight clean-up, but officials weren’t sure if more tar would show up. They planned to assess during low tide at midday.

Public health officials told people to avoid contact with the water, wet sand or any material that washed up in the area. They warned that contact with petroleum products can cause skin irritation and result in long-term health problems.

In the initial accounts, officials did not really have an idea of the magnitude of the spill or the potential aftermath of the spill.  The only concrete piece of knowledge that could be disseminated was that "tar balls" would show up?  Alright.  Furthermore, they closed the beach while cleanup crews walked the beach as shown in a photograph taken from the article and shown below:

Source: The Guardian

Can you imagine the concerted effort that was involved in order to get the oil removed from the beach?





A month later, the news was no less reassuring that the cleanup effort was successful thus far.  In another article appearing on the website "The Guardian" titled "Cleanup Of California Oil Spill Goes Low Tech To Limit Environmental Impact," the estimate of the total cleanup was to be around $64 million dollars -- wow!  That did not include the potential damage of the spill on the environment.  Here is an excerpt from that account regarding the cleanup effort at the time:

In the latest spill, workers shoveled tar balls and contaminated sand into plastic bags that were then carried away for disposal. They also had to be careful not to disturb populations of western snowy plovers that were in the middle of their breeding season.

 “We’re more concerned about the impact of the cleanup doing more injury than the oil did originally,” said Kim McCleneghan of the state department of fish and wildlife, who responded to both spills. 

About 91% of 97 miles of coastline – mostly sandy beaches – surveyed by teams of experts from various federal and state agencies has been given the all-clear.

Since the accounts surrounding the oil spill (within a few months), the subject has gone dark.  Meaning, that the news agencies are not spending coverage on the aftermath -- a year later.  That was (so I thought over the weekend after peeling oil off of my feet) until yesterday.

Plains All American Oil Gets Fined

An article that appeared in the "New York Times" titled "Company Says It's Been Indicted For The California Oil Spill" with a picture that reminded us of the extent of the spill shown below:

Source: New York Times

We are reminded of the extent of the damage of the oil spill by the excerpt shown below which was taken from the article:

On May 19 last year, the corroded, two-foot-diameter underground pipeline broke open near Refugio State Beach, west of Santa Barbara. Much of the oil flowed into the ocean, in an area that is home to an array of shorebirds and marine mammals, and is near the migratory path of gray whales. It formed a dark plume in the water that stretched for miles and coated several beaches, harming tourism, and officials have said that tar balls from the spill washed ashore as far as 100 miles to the southeast. 

The company initially estimated the spill at 21,000 gallons, but later revised that to more than 140,000 gallons. In documents supplied to lawmakers, Plains acknowledged that it had not alerted federal regulators until more than three hours after discovering the spill.

Here is an excerpt from the article discussing the possible distribution of charges being brought by the Attorney General of California -- Kamala Harris:

The California attorney general, Kamala D. Harris, and the Santa Barbara County district attorney, Joyce E. Dudley, said a Santa Barbara County grand jury had handed up an indictment charging the company, Plains All American, with four felonies and 42 misdemeanors, and charging an employee, James Buchanan, an environmental and regulatory compliance specialist at Plains, with three misdemeanors.

The company also faces multiple civil cases in the oil spill, but criminal charges in such a case are more unusual. Ms. Harris, who is running for the United States Senate, said the indictment reflected what the company knew or should have known of the dangers posed by its actions.

“The negative impacts of this conduct were immediate and tragic,” Ms. Harris said. “Anyone who violates the law and endangers our environment is going to be held responsible.”

I am happy to see that justice is being served toward the giant oil company "Plains All American Oil" by the Attorney General.  Accidents like this should not ever go away with time.  Especially, since the environmental destruction takes time to assess and set in.  After reading these articles and revisiting the oil spill, I wondering why I happened to get oil on my feet last weekend?

Oil Seeps Naturally From The Ocean Floor?

After I had the experience (which was foreign to me) of obtaining "tar" on my foot at the beach, I started to ask around.  I found a correlation with the information obtained about the presence of "tar" on the beach and the amount of years a person had been a resident of California.  Which is to say, people who had lived here less than 10 years tended to blame the "tar" on "natural oil seeps."  This fascinated me since I had lived here and frequented the beaches up and down the coast and not once (until this time) experienced "tar" on the beach.




Yes, I knew that there had been oil rigs up and down the coastal land (slightly inland) that had come and gone.  Still, I was surprised to hear from people how they just blew off the presence of "tar" as a derivative of the following statement: "Oh, the tar?  That is caused by natural oil seeps..."  What?  I guess that the following line of reasoning might be due to the amount of oil rigs that are in the area coupled with natural places like the La Brea Tar pits.  I highlighted the astounding amount of oil rigs in LA county in a previous blog post -- 5000 -- WOW.  With this number in mind, I guess that awareness should not make my discovery a surprise.




What about "natural oil seeps?"




I started to look into these "natural oil seeps."  What I found was an institute dedicated to studying the marine ecological environment called the "Woods Hole Oceanographic Institute."  The vision of the institute is stated below:

The ocean is a defining feature of our planet and crucial to life on Earth, yet it remains one of the planet’s last unexplored frontiers. For this reason, WHOI scientists and engineers are committed to understanding all facets of the ocean as well as its complex connections with Earth’s atmosphere, land, ice, seafloor, and life—including humanity. This is essential not only to advance knowledge about our planet, but also to ensure society’s long-term welfare and to help guide human stewardship of the environment. WHOI researchers are also dedicated to training future generations of ocean science leaders, to providing unbiased information that informs public policy and decision-making, and to expanding public awareness about the importance of the global ocean and its resources.

The WHOI in abbreviated form was instrumental in the analysis of the BP Gulf Deepwater Horizon Oil spill 6 years ago.  That spill was the largest oil spill in history.  The institute played a major role in analyzing the plankton and other marine organisms trapped in water columns near the blowout of oil along with the overall oil dispersion over time within the ocean.  The main take home message of me bringing this up is to say that the WHOI has experience with "natural oil seeps" -- studying the origination and contribution to the environment.  Check out their "Research Projects" page.




After I delved into their website a little more, I found statements like the one below discussing the origination of oil in the ocean which surprised me:

Oil can come from a variety of sources, each of which influences the amount, type, and duration of a spill. The 2003 report published by the National Research Council titled Oil in the Sea III organized these sources into four categories: natural seeps, petroleum extraction, petroleum transportation, and petroleum consumption. Of these, seeps are by far the single largest source, accounting for nearly half of all the petroleum compounds released to the ocean worldwide each year. Seeps are also the only natural source of oil input to the environment. The other sources, in order of magnitude, are extraction, transportation, and consumption and stem from human activity.

An important difference between seeps and human-generated inputs is that seeps are widely distributed around the world and occur at a fairly slow and relatively constant rate.  So constant, in fact, that some animals and microbes have evolved to thrive in the presence of the chemicals that flow from the seafloor near seeps. Studies of these unique organisms and ecosystems are an important part of the picture that scientists are assembling of how oil affects marine biology.

Oil that enters the ocean as a result of extraction, transportation, or consumption often receives more attention than seeps for the simple fact that it is more visible. These events are of interest to scientists because they generally constitute large inputs from a single source and can occur anywhere in the world, often in places that have little, if any, natural ability to cope with the contamination. The impacts of oiling on individual plants and animals or on entire ecosystems range from the visible and immediate (e.g., smothering) to long-term and largely hidden (e.g., genetic disruption) and can have implications on the physical structure or health of a region for decades. Human systems, such as water supplies, fisheries, and tourism industries, are also vulnerable to oil spills, and this adds even more complexity when trying to understand the full effects of a particular event.

I was surprised to find out that nearly half of the oil in the ocean comes from natural inputs.  I am still skeptical of the situation.  Upon further research into their website, the sources of oil become more apparent and justified from a scientific standpoint.  I want to show an excerpt that will bring to light a more logical connection to my experience at Venice Beach a couple of weekends ago.  Here is the excerpt from the "natural oil seeps" webpage on the WHOI website:

In locations where seeps are found, oil flows slowly up through networks of cracks, forming springs of hydrocarbons similar to the La Brae tar pits on land. Lighter compounds rise buoyantly to the water’s surface and evaporate or become entrained in ocean currents; others fall to the seafloor and collect over hundreds or thousands of years. 

Seeps are often found in places where oil and gas extraction activities are also located. As a result, many surface slicks and tar balls caused by seeps are often attributed to releases from oil and gas platforms. The question arises, then: If oil occurs naturally in the ocean and if seeps are the biggest single source, why is there concern about the occasional accidental spill? The answer lies in the nature and rates of oil inputs by these different sources.

Seeps are generally very old and flow at a very low rate. The material that flows out is still very often toxic, but organisms some that live nearby are adapted to conditions in and around seeps. A few very unique species of animals are even able to use the hydrocarbons and other chemicals released at seeps as a source of metabolic energy. In addition, rather than being made up entirely crude oil, the material flowing from seeps is often heavily biodegraded by microbial action deep beneath the seafloor.

In contrast, the production, transportation, and consumption of oil by humans generally results in relatively short, high-volume inputs of oil and refined hydrocarbon products in places that have never experienced significant exposure to these chemicals and so do not have many natural defenses to them. As a result, seeps are often looked upon as a living laboratory for scientists to study how natural processes affect the fate of released oil or how individual species or communities of plants and animals are capable of dealing with the burden of otherwise toxic chemicals. From this may one day come a better understanding of how to help places affected by oil spills recover and regain much of their pre-spill health and function.

These last four paragraphs justify my experience at the beach a couple of weeks ago.  Within the excerpt above, the contribution from the extraction and transport processes play a large role in the "tar" encountered on the beaches.  Additionally, this coincides with the statements I have heard since my experience from older "locals" of the Los Angeles area.  Some will not even go into the water anymore to surf because of the oil "tar" -- which has increased over the years.  This brings me to my last question:




Why has no one mentioned the increase in "tar" on the beaches or reported on the increase?




Have we all lost our minds? And as a result are just accepting of this unusual occurrence?




Something is unusual here.  I am very surprised that not one of these communities along the coast (Malibu, Santa Barbara, Manhattan, Santa Monica, etc.) have not been outraged at the increased occurrence of "tar" on the beaches.  Simply amazing.

Conclusion...

I remain skeptical of the contribution of the "natural oil seeps" due to the science of the flow rate and leakage along with the evolution of natural organisms to capitalize on their location and use the various hydrocarbons for nutrients.  This seems to me to be natural. Yet, these organisms would not leave behind giant "tar balls" to be washed up onto shore.  And if so, why would generations not be complaining about the presence of such organic matter on the shore.




The beaches in California are nearly worshipped along with the weather.  Over the generations, I am surprised to not hear anything of these natural occurrences.  Therefore, I tend to favor the other opinion that I hold -- the big oil companies are to blame for the increase in "tar" on our beaches.  With the presence of the "fall out" from last year's 140,000 gallons, I am more inclined to attribute the increase in "tar" to events such as those (as terrible as they may be).




Last Thursday, KPCC (a radio station) had a story titled "Pipeline Operator Could Face Additional Penalties For Santa Barbara Oil Spill" which talked about the disaster briefly and the "final investigative report" released by authorities regarding the Plains All American Pipeline's failure in last year's oil spill.  Here was the introduction to the story below which justifies my skepticism regarding a greater contribution from "Big Oil" rather than "natural oil seeps":

An oil pipeline company responsible for a massive spill on the California coast a year ago didn't do enough to prevent corrosion and its operators didn't detect and react to the spill quickly enough, federal regulators said Thursday.

Plains All American Pipeline also didn't have adequate systems in place to signal there was a major leak in the pipeline running near the Santa Barbara County coast, the Pipeline and Hazardous Materials Safety Administration said in its final investigation report.

"The operators failed on multiple levels to prevent, detect and respond to this incident," agency Administrator Marie Therese Dominguez said. "A number of preventable errors led to this incident and the company's failures in judgment, including inadequate assessment of this line, and faulty planning made matters worse. What happened is completely unacceptable and we will hold the company accountable."

I think that enough has been said on the matter.  What is next is the litigation followed by action.  What does "action" look like?  Well, each of us need to follow horrible stories like this and take "action" by writing (e-mail or written letter, or call) our local representatives and explain that these events do not justify the drilling that is going on currently.  All oil drilling should be shut down in the region until an agreement between large oil companies and agencies along with the public can be reached.




How much more of the environment do we need to damage before the message is heard?  As of this moment, the public and legislatures appear to be wearing "ear muffs" to buffer out the noise (outcry) of this damaging action by the oil companies.   Until next time, your assignment is to read more about the oil seeps and the part that "Big Oil" is playing into them.  Have a great day.

Are The Elements Hydrogen And Helium "Of This World"?

Have you seen the image shown below on a t-shirt or a bumper sticker on a vehicle?  How about a tattoo of the image?

Source: Brands of the World

I remember being thoroughly confused the first time that I saw the image on the back of a truck's window.  Of course, I was equally confused when I saw the word "YOLO" in print the first time too.  "YOLO" means "You Only Live Once."  "NOTW" means "Not Of This World."  There are many of these little shortened statements floating around the internet.  Why is "NOTW" important and used in the same title as the chemical elements Hydrogen and Helium?  Great question.




Short answer: Read the paragraphs below to find out!




Long answer: The other day I was thinking about the concept of "escape velocity" and these two elements came to mind.  If set free, will each of the elements in gaseous form leave "our world" -- the atmosphere around planet Earth?  In the answer is yes, then these two elements are "Not Of  This World."  First, lets focus on the crucial question: Why does the escape occur?  What properties allow that to happen?  The answers are contained in the paragraphs below.

Escape Velocity?

If you were to go outside onto your yard lawn and jump up into the air, what would happen?  You would probably briefly rise up into the air and then begin to descend back onto the lawn.  Why?  The reason is due to the Earth's gravitational field.  As I wrote in an earlier post on force, the gravitational field is exerting a force to accelerate your body onto the surface of the Earth.   This is Newton's Law of Universal Gravitation and can be represented by the equation below:

where 'm' is the mass and 'g' is vector representing the acceleration of gravity with a constant magnitude of 9.81 m/s^2 (meters per second squared) toward Earth.  Why is this important?  Well, you would have to understand the effects of gravity if you were going to launch a spacecraft into space right?  You would have to plan to overcome the gravitational field in a safe manner without destroying your spaceship in the process?  The general equation for a Force on mass-1 due to the gravitational pull of mass-2 can be represented by the following equation shown below:

Where G is the gravitational constant and the two masses experiencing this pull between one another are represented by m1(mass-1) and m2 (mass-2).  Furthermore, the strength of the gravitational force varies by the inverse of the square of the distant between the two masses.  Simply stated right.  Therefore, to escape this force, energy would be needed.




How does one calculate the escape velocity for an object to leave the atmosphere?




In order to break the gravitational barrier, the proper energy must be obtained.  Two questions need to be answered in order to arrive at a escape velocity:




1) How much energy is required to break the gravitational barrier?




2) How much kinetic energy is required to break the gravitational barrier?




A this point you might be slightly confused.  I just showed you an equation for the force between two masses with a gravitational pull.  Now, I am asking about kinetic energy?  Where is the connection between the two?  Fair enough.




To start with, the force is holding us on the planet.  As a thought experiment, we can think of a rock on top of a mountain.  That rock has a large amount of potential energy.  If that rock were to roll down the mountain, the potential energy would be converted into kinetic energy.  In order to drive the point home, an excerpt from the "Wikipedia" page for "potential energy" might help the reader understand the work (energy) required to break the gravitational field is shown below:

There are various types of potential energy, each associated with a particular type of force. For example, the work of an elastic force is called elastic potential energy; work of the gravitational force is called gravitational potential energy; work of the Coulomb force is called electric potential energy; work of the strong nuclear force or weak nuclear force acting on the baryon charge is called nuclear potential energy; work of intermolecular forces is called intermolecular potential energy. Chemical potential energy, such as the energy stored in fossil fuels, is the work of the Coulomb force during rearrangement of mutual positions of electrons and nuclei in atoms and molecules. Thermal energy usually has two components: the kinetic energy of random motions of particles and the potential energy of their mutual positions.

In equation form, the potential energy is shown as follows:

Again, to launch into space, the potential energy (stored energy) needs to be converted into 100% kinetic energy (the energy of motion).  Following this line of reasoning leave us to equate the two energies as shown below:

To determine the escape velocity needed to break the Earth's gravitational pull.  Before the above equation is rearranged to solve for "v" -- velocity, one more substitution needs to be made.  The substitution is an expression for the gravitational acceleration at the surface of the earth.  Below is an expression to substitute for G in the equation above:

If the above expression is substituted into the equation for gravitational potential energy, the expression below is the relation of the energy needed to escape the surface of the Earth:

Now, the above expression is the escape velocity required to leave the Earth's gravitational pull.  The remaining task is to plug numbers into the equation and calculate the velocity as shown below:

There you have the answer.  In order to break Earth's gravitational pull, an object (i.e., spaceship, molecules, atoms, etc.) needs to travel at minimum escape velocity of 7 miles per second.  Take a look at a map.  Look for a landmark or geographical point that is 7 miles away from your house.  Imagine, traveling that distance in one second.  Wow!




That sets the discussion in motion with a definite answer.  The space shuttle carries fuel which helps propel it into orbit.  Are there any natural objects that might possess enough energy to escape the Earth's atmosphere without fuel?  I cannot think of any off the top of my head that travel normally at 7 mile/sec.  That is what I would expect to hear from most people.  Sub-atomic particles travel quickly.  Entertaining this question, I recalled hearing years ago that both chemicals -- Helium and Hydrogen possess enough energy to escape the atmosphere.




A couple of weeks ago, I wrote a blog post about cooking pasta like a chemist.  The point of that post was to inspire people to imagine the dynamic environment that is occurring in the boiling water and the headspace just above it.  While writing that post, I could not help but to return to the statement that I had heard several years earlier regarding both chemicals -- Helium and Hydrogen -- possessing enough energy to escape Earth's gravitational field.   I started narrowing my curiosity down to the following question:




What properties enable the elements hydrogen and helium to escape the Earth's atmosphere?




Are these two chemicals special?  Do other chemicals possess enough energy to escape Earth's gravitational field?




The answer is interesting but somewhat complex and still being researched.  Below, I start to discuss the parameters which might give both of these chemicals the ability to act special (in the sense of escaping into space).  Read on below to find out the answer.

Hydrogen & Helium Are Special!

As I found out, the process is simple yet complicated.   How does that figure?  Simple yet complicated?  In order to understand the statement about these elements, we must take a divergent step for a brief backstory in chemistry.  These two elements are gases at room temperature.  In order to describe the behavior of the gases at a particular temperature, the "probability distribution" created by James Clerk Maxwell must be shown to illustrate our point.  First, lets read the description of the "probability distribution" of molecular speeds devised by him taken from "Wikipedia":

In statistics the Maxwell–Boltzmann distribution is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann. It was first defined and used in physics (in particular in statistical mechanics) for describing particle speeds in idealized gases where the particles move freely inside a stationary container without interacting with one another, except for very brief collisions in which they exchange energy and momentum with each other or with their thermal environment. Particle in this context refers to gaseous particles (atoms or molecules), and the system of particles is assumed to have reached thermodynamic equilibrium.[1] While the distribution was first derived by Maxwell in 1860 on heuristic grounds,[2] Boltzmann later carried out significant investigations into the physical origins of this distribution.

A particle speed probability distribution indicates which speeds are more likely: a particle will have a speed selected randomly from the distribution, and is more likely to be within one range of speeds than another. The distribution depends on the temperature of the system and the mass of the particle.[3] The Maxwell–Boltzmann distribution applies to the classical ideal gas, which is an idealization of real gases. In real gases, there are various effects (e.g., van der Waals interactions, vortical flow, relativistic speed limits, and quantum exchange interactions) that can make their speed distribution different from the Maxwell–Boltzmann form. However, rarefied gases at ordinary temperatures behave very nearly like an ideal gas and the Maxwell speed distribution is an excellent approximation for such gases. Thus, it forms the basis of the Kinetic theory of gases, which provides a simplified explanation of many fundamental gaseous properties, including pressure and diffusion.[4]

The distribution is very useful in describing the behavior of "ideal gases".  In this context, helium is considered an "ideal gas" -- why you might ask?  Because one of the properties of the helium molecule is "inertness".  What does this mean?  Typically, that helium does not react with other gases.   On a side note, helium is very useful in carrying out chemical reactions that are "air sensitive." Helium gas is "inert" and serves the purpose of providing an "reactive" free environment in which desired chemicals can be introduced to carry out a chemical reaction.  What do I mean by this?  In the photograph below, there is a picture of a graduate student carrying out a chemical reaction in a "glove box" which is "air sensitive" -- the atmosphere in this case is Argon -- another "inert gas":

 Using an environment of helium or nitrogen or argon is common in any chemistry department in the world.




What does this "probability distribution" look like?




Shown below is the general representation of Maxwell's Distribution of molecular/atomic Speeds:

Source: Pdbailey at English Wikipedia

As you can see, the distribution is greatly dependent on molecular weight.  A heavier element like Xenon with a molecular mass of 131.293 grams/mole has a narrow range of speeds (0-500 m/s).  Whereas the element Argon has a molecular mass of 40 grams/mole and a broader distribution (0-900 m/s).  The lightest of the "Noble gases" is helium with a molecular mass of 4 grams/mole and a broad distribution (0-2500 m/s).




From this information, you should be able to compare the highest speed with that of the escape velocity needed to break the gravitational field from the previous calculations above for a space ship.  Additionally, the other variable that determines the shape and location (i.e., the speed) is the temperature.  After a brief search "online" I was able to find a good representation of the "probability distribution" dependency on temperature.  For a given gas at two different temperatures, "OpenStax" has a great diagram shown below:

Source: OpenStax

Notice how the average speed of the molecule changes along with the top speed (determined by the tail of the distribution length) shown in the colors red and green.  At higher temperatures, the distribution gets broad and the top speed is much greater.  This is important in understanding how the gases act in the upper atmosphere.  Naturally, at this point, you are probably asking yourself, how high would the temperature have to be to eject (play a dominant role) in the escape velocity.

What about temperature?

In order to calculate the temperature needed to provide enough thermal energy to eject a molecule of helium or hydrogen, an expression is needed for the speed of molecules at a given temperature.  For this, the analysis of the "probability distribution" (breaking down the nature of the distribution curves) yields a "root-mean-square" speed of the following form:

In order to calculate the temperature, the above expression needs to be rearranged to solve for temperature T as follows:

Plugging in the remaining values for the mass of the Earth, M, the "root-mean-square" speed, and the gas constant, R, yields the following:

That is hot!  Does the atmospheric temperature ever reach the above temperature?  Hopefully, not -- at least in the lower atmosphere.  Further, the temperature does not reach this value along the distribution of height with temperature.  Therefore, the only way to obtain enough energy to escape is through interacting in the complex upper atmosphere.




There are a number of factors along with the collisional energy that allow both molecules (hydrogen and helium) to escape.  For the purposes of this post, we will focus on the dominant factor -- collision energy.




How does a person visualize this complexity within the atmosphere above them?




Look up into the sky.  If the weather calls for a storm, then there will be clouds and just by inspection, the situation does not look good.  Clouds help us visualize the complexity going on in the sky at any given moment.  The shape gives us insight into the various patterns of wind moving around at various heights.  Although, we are not able to perceive the depth of various patterns from the ground.  Can we do better?




Sure, watch the weather channel with the satellite images.  Shown below is a short video of a satellite image of a storm moving through the Southern California region.  Watch how the storm moves across the region.




On the screen, the movement appears to be slow.  But, if you had a sensor up in the sky, the situation might appear to be much more chaotic.  Why is this realization important?  Because, according the the explanation above based on the distribution of speeds of gases at a given temperature, even the lightest gases (hydrogen and helium) lack sufficient energy to overcome the barrier to escape the atmosphere.  Naturally, this leads up to the following question:




Where does the remainder of the kinetic energy come from?




I was thinking about this while walking through campus over the last few days.  Suddenly, I realized that the complexity in the atmosphere might easily be understood (visually) by looking at the state Lottery.  Yes, the lottery.  If you take a look at the short video (less than 30 seconds)below of the lottery drawing, you will see a container with balls that are being mixed quite rapidly.









If we were to remove the hype of the lottery and focus on the experiment (balls being mixed inside a container), then we should focus on the video below.  Shown below is a video of just the "SmartPlay" lottery mixer:








As you can see, there is a large amount of kinetic energy in the system to begin with which is being supplied by the air to mix the balls in the container.  When the time comes to draw a ball -- which is indicated by one ball being "ejected" up the center column and held by air to be read by the lottery announcer.  The balls in the container could be compared to the atoms and molecules that are being mixed by the wind currents (in addition to the Earth's rotational energy contribution).  The Earth rotates at a speed of around




The process of "ejecting" the ball could be analogous to a "chaotic current" in the upper atmosphere which would give the helium molecule enough energy to overcome the remainder of the barrier to the appropriate escape velocity of 7 miles/sec.




Formally, the bridge that connects Maxwell's Distribution of speeds with the escape velocity was introduced by a physicist named James Jeans.  According to "Wikipedia," the mechanism of "Jeans escape" is a thermal contribution from the solar energy.  Here is an excerpt:

One classical thermal escape mechanism is Jeans escape.[1] In a quantity of gas, the average velocity of a molecule is determined by temperature, but the velocity of individual molecules change as they collide with one another, gaining and losing kinetic energy. The variation in kinetic energy among the molecules is described by the Maxwell distribution.

The kinetic energy and mass of a molecule determine its velocity by E_{\mathit{kin}}=\frac{1}{2}mv^2.

Individual molecules in the high tail of the distribution may reach escape velocity, at a level in the atmosphere where the mean free path is comparable to the scale height, and leave the atmosphere.

The more massive the molecule of a gas is, the lower the average velocity of molecules of that gas at a given temperature, and the less likely it is that any of them reach escape velocity.

This is why hydrogen escapes from an atmosphere more easily than carbon dioxide. Also, if the planet has a higher mass, the escape velocity is greater, and fewer particles will escape. This is why the gas giant planets still retain significant amounts of hydrogen and helium, which have largely escaped from Earth's atmosphere. The distance a planet orbits from a star also plays a part; a close planet has a hotter atmosphere, with a range of velocities shifted into the higher end of the distribution, hence, a greater likelihood of escape. A distant body has a cooler atmosphere, with a range of lower velocities, and less chance of escape. This helps Titan, which is small compared to Earth but further from the Sun, retain its atmosphere.

An atmosphere with a high enough pressure and temperature can undergo a different escape mechanism - "hydrodynamic escape". In this situation the atmosphere simply flows off like a wind into space, due to pressure gradients initiated by thermal energy deposition. Here it is possible to lose heavier molecules that would not normally be lost. Hydrodynamic escape has been observed for exoplanets close-to their host star, including several hot Jupiters (HD 209458b, HD 189733b) and a hot Neptune (GJ 436b).

Interestingly enough, the variation of the speeds in the Maxwell distribution are similar to the deficit of Professor Jeans idea regarding the loss of gases to space.  According to measurements made after he passed, the escape mechanism (based on thermal energy) cannot account for all of the gas that has escaped the orbit.  Therefore, we are left with other mechanisms at play that contribute energy -- known and others that are unknown (i.e. still being researched).




As I mentioned at the beginning of the section regarding the elements hydrogen and helium, the dynamics are complex.  Amazingly enough, contributions from insightful physicists such as James Clerk Maxwell and James Jean have withstood the test of time and held up as a significant contribution to evaluating molecular speeds based on temperature, molecular mass, and gravitational pull.  How the gravitational system contributes to the escape of the distribution (the tail of the distribution without sufficient energy to obtain escape velocities) remains to be discovered?

Conclusion...

The dynamics are complex in the atmosphere above us.  I say that not as an excuse, but a challenge to conquer them in the future.  Find out what types of collisional energy contribute the escape velocity of a hydrogen atom.  Why do other "heavier" molecules escape sometimes?  How do other collisional exchanges contribute -- Rotational energy, Translational energy, etc.?  How does the Earth's rotation contribute to the escape velocity of these small molecular systems?




One take-away message is concrete among many uncertain.  That is, our ability to send a manned space shuttle into space without problems of breaking the gravitational pull is absolutely amazing.  Our technological development has led us to understand the atmosphere to a large extent.  As you can see, there is still a lot of room to grow intellectually.  This is where each of us come in.  We need to continue to opt for funding for space programs.  As I will discuss in future posts, many technological developments are created as a result of such research.  Until then, keep on learning as much as you possibly can about the world.  Have a great weekend.