"Newton's First Law of Motion states that a body at rest stays at rest unless an outside force disturbs it. Today, this maxim helps illuminate why people are on the move: External forces--wars, rising seas, feeble economies--have dispossessed hundreds of millions of refugees and migrants now living outside their home countries. But what does it mean to survive an uprooting? Drawing on unique, even surprising perspectives, this issue of FP examines human endurance and how it shapes the global landscape. ..."
What kind of force can cause the described events above? How do we describe the force that can cause these events? As with any description of an event, there will be associated 'units' used to put the event into context. What do I mean by this? Below, I will describe a couple of events or situations and use the appropriate 'units' to describe them.
What Is A Kiloton?
Recently, the unit of kiloton has been showing up to describe large amounts of energy or force released in a given event. Whether that event be a 'nuclear test' as in North Korea last month or that be an astronomical event -- the 'kiloton' is the appropriate unit to contextualize such an event. A couple of months ago, I wrote a blog about the amount of energy contained within a 'kiloton' of energy. Just a week ago, I got an e-mail from 'Harper's' magazine with the following factoid shown below containing a kiloton:
A meteor exploding over planet Earth with a force equivalent to that of the force given off by the explosion of 13,000 tons of TNT. Expressed more succinctly, the force given off by 13-kilotons of TNT.
Energy and force are different but related through the concept of 'work' (taken from 'wikipedia'):
In physics, a force is said to do work if, when acting on a body, there is a displacement of the point of application in the direction of the force. For example, when a ball is held above the ground and then dropped, the work done on the ball as it falls is equal to the weight of the ball (a force) multiplied by the distance to the ground (a displacement).
If we restrict ourselves for a moment to just talk about the 'interaction' of the 'force' and the 'body' then the definition of 'force' is as follows (taken from 'wikipedia'):
In physics, a force is any interaction that, when unopposed, will change the motion of an object.[1] In other words, a force can cause an object with mass to change its velocity (which includes to begin moving from a state of rest), i.e., to accelerate. Force can also be described by intuitive concepts such as a push or a pull. A force has both magnitude and direction, making it a vector quantity. It is measured in the SI unit of newtons and represented by the symbol F.The original form of Newton's second law states that the net force acting upon an object is equal to the rate at which its momentum changes with time. If the mass of the object is constant, this law implies that the acceleration of an object is directly proportional to the net force acting on the object, is in the direction of the net force, and is inversely proportional to the mass of the object
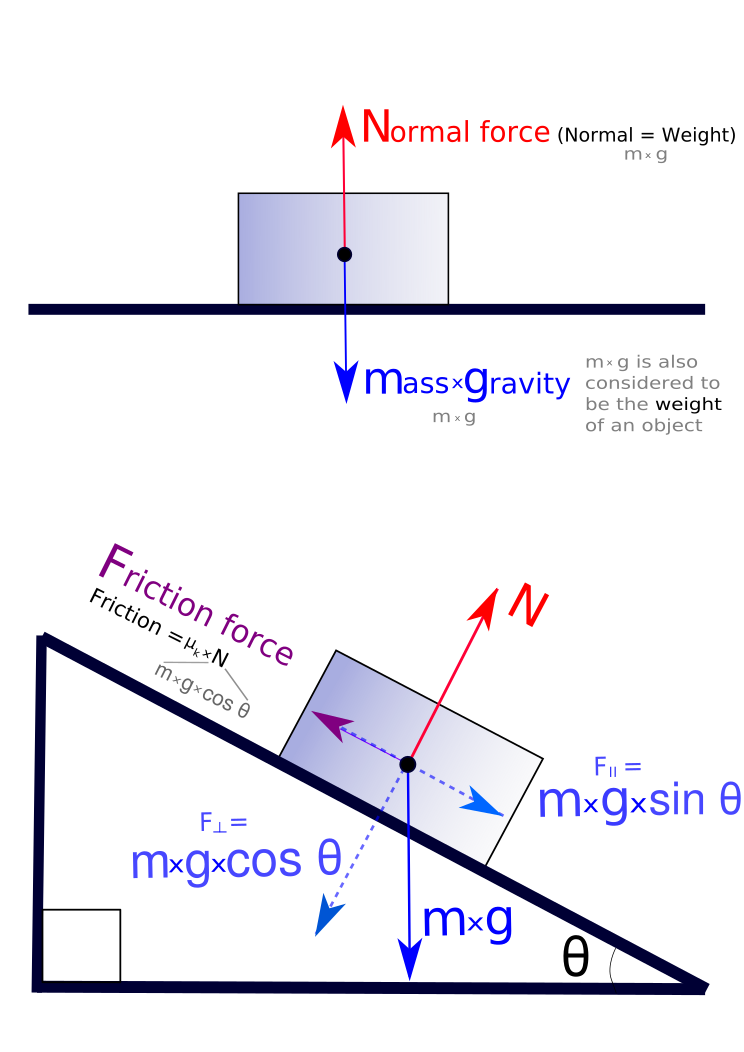
The application of a force over a given distance is equal to the work done. To express the directionality and magnitude of the force requires vector quantities. To use a simple example, here is a picture of a two different objects resting on surfaces with the relevant forces outlined (taken from 'Wikipedia') -- shown below:
Diagram by Penubag
Each of the two situations show a mass resting on a surface. In the upper diagram, the mass (a box) is resting on a flat surface. Whereas, in the second diagram, the mass is shown on a tilted surface or a diagonal surface. The difference between the two represents the difference in directionality of the applied force on the surface. Think about standing on a floor. What happens when you try to stand on a slide at a playground?
Here is a description from 'Wikipedia' that caught my eye shown below:
Forces act in a particular direction and have sizes dependent upon how strong the push or pull is. Because of these characteristics, forces are classified as "vector quantities". This means that forces follow a different set of mathematical rules than physical quantities that do not have direction (denoted scalar quantities). For example, when determining what happens when two forces act on the same object, it is necessary to know both the magnitude and the direction of both forces to calculate the result. If both of these pieces of information are not known for each force, the situation is ambiguous. For example, if you know that two people are pulling on the same rope with known magnitudes of force but you do not know which direction either person is pulling, it is impossible to determine what the acceleration of the rope will be. The two people could be pulling against each other as in tug of war or the two people could be pulling in the same direction. In this simple one-dimensional example, without knowing the direction of the forces it is impossible to decide whether the net force is the result of adding the two force magnitudes or subtracting one from the other. Associating forces with vectors avoids such problems.
Now that we know that force has "directionality" (vector quantity) and magnitude (scalar quantity), lets return to the example of a person standing on a surface. The Direction and magnitude of the applied force matter when defining a system. How about using the human body as an example to illustrate the definition of force? When each of us wakes up in the morning and gets out of bed, we assume that the floor beneath us will hold us up right? I weigh around 180 pounds. That means that my weight on the floor is equal to 180 pounds multiplied by the acceleration of gravity.
We know that gravity holds us to the ground -- right? Newton's Second Law of Motion allows us to measure the force on an object knowing that the mass is constant. Also, we know that if the forces are balanced, we should remain standing up. The force that I exert by standing on the ground is calculated as follows:
I am exerting a force of ...Newtons on the ground. If I am standing straight up then the force is straight down. Additionally, the ground is pushing up ...Newtons to hold me up. Otherwise, I would fall into or onto (depending on the angle of my body to) the ground. Here is a video showing the terrible situations that can arise in the construction world if the forces are not balanced. Check part of the video out. (It is long -- around 8 minutes):
In each of the cases in the video above, the forces were not balanced and the disaster was for the objects (trucks, tankers, tractors, etc.) to fall toward equilibrium. Now that I have provided a few background examples and information into the concept of force, lets return to the question at hand (the subject of the blog post): How much force is in a 'kiloton'?
To answer the question, we need to convert the mass of a kiloton to kilograms -- a unit conversion. The conversion is shown below:
These units are expressed for a mass. In the above diagram, the downward arrow has small writing next to it showing the following: "m x g is also considered to be the weight of an object." When discussing the concept of force, to distinguish between the two -- one must ask: "What units are weight expressed in?" If the unit is 'N' for Newtons, then the weight is being expressed as a force.
Therefore, in the above statement by NASA, is the force kiloton's of Newtons or kilotons x force (another unit). Statements can get confusing pretty easily. That is the importance of specifying 'units' of a measurement. Lets assume for a moment that the force is NOT expressed in Newtons. In order to calculate the force of a kiloton we would multiply the mass (a kiloton) by the acceleration of gravity as shown below:
The force of a kiloton is N. How can we better understand that number considering what has been explained above in terms of force and energy? In the video above, a number of situations were shown were the forces of the objects were not balanced properly. The imbalance resulted in the object being tilted or tipped on its size or sliding down a surface. Eventually, the object (tractor or trucks) came to an "equilibrium" state of rest where the forces acting in all directions were "balanced" out. This is an important concept to understand.
Another way to view balancing forces is to imagine yourself standing up. Behind you is a bed. As you fall back onto the bed there are forces acting on yourself to eventually land on the bed. Given that the bed is underneath you. Eventually, as you land on the bed, the bed will exert a force upward (to hold you up) of your weight (mass x g). Force can be distributed in a variety of ways.
Pressure Wave Expressed As A Force
In the video above, the examples all indicate the imbalance of a force to stabilize an object. Whereas in the Harper's excerpt with the factoid of an asteroid bearing down upon the Earth with a force of 13,000 - kiloton is a distributive (pressure force). Upon an explosion, a wave of pressure (force over an area) is generated that exerts a force on any object in its path. Force is expressed as a function of pressure:
The pressure wave given off during an explosion is a force distributed over a given area. The magnitude of that force is representative of using the commonly found expression (or unit) of a kiloton. Whenever an explosion or a force has a tremendous amount of force or energy, the common unit seems to be expressed in kiloton(s). When force is distributed over the entire planet Earth, the result may by small. A major example in history is the dropping of a nuclear weapon over a small city -- Nagasaki, Japan -- in which the destruction is large as shown below:
Source: Wikipedia
The weapon that was dropped on the city of Nagasaki exploded from 1800 feet above ground. The weapon did not reach the ground before exploding. Still, as is shown in the images collected online, the damage was devastating to say the least. Today, great measures in diplomacy are taken to steer clear of the threat of "nuclear warfare" since the effects or aftermath are too devastating.
The point has been made. Force can be distributed in a variety of ways. We could ask the simple question: Could the force of a nuclear weapon lift the ship "Queen Mary"?
To answer the question without too many calculations, we would just need to know the weight of the ship. Here is a picture of the ship below:
Source: By David Jones
According to "Wikipedia," the Queen Mary weighs around 81,900 tons. Without performing a calculation and taking account the definition of "weight" from above, we could say NO. Again, how force is distributed is critical to answering the question.
Conclusion
The amount of force generated by a nuclear weapon may not be enough to lift up (off of the ground) the ship -- "Queen Mary" -- but is sufficient to level a small city. Directionality of a force can help define the magnitude of the resultant force. Concentration of pressure waves can also determine the extent of damage that a force can do. According to the equation for pressure above, a large force over a small area will exert a large pressure. Whereas a force distributed over a large area will be nearly not noticeable. Here is a closing picture to illustrate this point taken from "Wikipedia" that is somewhat familiar to each of us:
Source: http://entertainment.howstuffworks.com/arts/circus-arts/bed-of-nails.htm
The next time that you are challenged to consider the force of an object, consider the calculations in the post above. Further, think of how much force that you are exerting by standing on the floor at the current moment? The force coming from the asteroid is negligible due to the surface that the force was spread over. These are critical concepts to consider when forming a reaction to a situation.


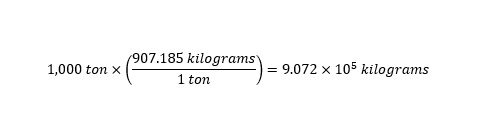
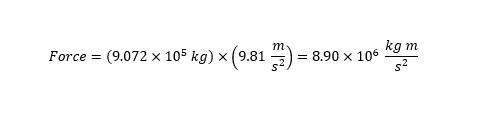




No comments:
Post a Comment