Source: Brands of the World
I remember being thoroughly confused the first time that I saw the image on the back of a truck's window. Of course, I was equally confused when I saw the word "YOLO" in print the first time too. "YOLO" means "You Only Live Once." "NOTW" means "Not Of This World." There are many of these little shortened statements floating around the internet. Why is "NOTW" important and used in the same title as the chemical elements Hydrogen and Helium? Great question.
Short answer: Read the paragraphs below to find out!
Long answer: The other day I was thinking about the concept of "escape velocity" and these two elements came to mind. If set free, will each of the elements in gaseous form leave "our world" -- the atmosphere around planet Earth? In the answer is yes, then these two elements are "Not Of This World." First, lets focus on the crucial question: Why does the escape occur? What properties allow that to happen? The answers are contained in the paragraphs below.
Escape Velocity?
If you were to go outside onto your yard lawn and jump up into the air, what would happen? You would probably briefly rise up into the air and then begin to descend back onto the lawn. Why? The reason is due to the Earth's gravitational field. As I wrote in an earlier post on force, the gravitational field is exerting a force to accelerate your body onto the surface of the Earth. This is Newton's Law of Universal Gravitation and can be represented by the equation below:
where 'm' is the mass and 'g' is vector representing the acceleration of gravity with a constant magnitude of 9.81 m/s^2 (meters per second squared) toward Earth. Why is this important? Well, you would have to understand the effects of gravity if you were going to launch a spacecraft into space right? You would have to plan to overcome the gravitational field in a safe manner without destroying your spaceship in the process? The general equation for a Force on mass-1 due to the gravitational pull of mass-2 can be represented by the following equation shown below:
Where G is the gravitational constant and the two masses experiencing this pull between one another are represented by m1(mass-1) and m2 (mass-2). Furthermore, the strength of the gravitational force varies by the inverse of the square of the distant between the two masses. Simply stated right. Therefore, to escape this force, energy would be needed.
How does one calculate the escape velocity for an object to leave the atmosphere?
In order to break the gravitational barrier, the proper energy must be obtained. Two questions need to be answered in order to arrive at a escape velocity:
1) How much energy is required to break the gravitational barrier?
2) How much kinetic energy is required to break the gravitational barrier?
A this point you might be slightly confused. I just showed you an equation for the force between two masses with a gravitational pull. Now, I am asking about kinetic energy? Where is the connection between the two? Fair enough.
To start with, the force is holding us on the planet. As a thought experiment, we can think of a rock on top of a mountain. That rock has a large amount of potential energy. If that rock were to roll down the mountain, the potential energy would be converted into kinetic energy. In order to drive the point home, an excerpt from the "Wikipedia" page for "potential energy" might help the reader understand the work (energy) required to break the gravitational field is shown below:
There are various types of potential energy, each associated with a particular type of force. For example, the work of an elastic force is called elastic potential energy; work of the gravitational force is called gravitational potential energy; work of the Coulomb force is called electric potential energy; work of the strong nuclear force or weak nuclear force acting on the baryon charge is called nuclear potential energy; work of intermolecular forces is called intermolecular potential energy. Chemical potential energy, such as the energy stored in fossil fuels, is the work of the Coulomb force during rearrangement of mutual positions of electrons and nuclei in atoms and molecules. Thermal energy usually has two components: the kinetic energy of random motions of particles and the potential energy of their mutual positions.
In equation form, the potential energy is shown as follows:
Again, to launch into space, the potential energy (stored energy) needs to be converted into 100% kinetic energy (the energy of motion). Following this line of reasoning leave us to equate the two energies as shown below:
To determine the escape velocity needed to break the Earth's gravitational pull. Before the above equation is rearranged to solve for "v" -- velocity, one more substitution needs to be made. The substitution is an expression for the gravitational acceleration at the surface of the earth. Below is an expression to substitute for G in the equation above:
If the above expression is substituted into the equation for gravitational potential energy, the expression below is the relation of the energy needed to escape the surface of the Earth:
Now, the above expression is the escape velocity required to leave the Earth's gravitational pull. The remaining task is to plug numbers into the equation and calculate the velocity as shown below:
There you have the answer. In order to break Earth's gravitational pull, an object (i.e., spaceship, molecules, atoms, etc.) needs to travel at minimum escape velocity of 7 miles per second. Take a look at a map. Look for a landmark or geographical point that is 7 miles away from your house. Imagine, traveling that distance in one second. Wow!
That sets the discussion in motion with a definite answer. The space shuttle carries fuel which helps propel it into orbit. Are there any natural objects that might possess enough energy to escape the Earth's atmosphere without fuel? I cannot think of any off the top of my head that travel normally at 7 mile/sec. That is what I would expect to hear from most people. Sub-atomic particles travel quickly. Entertaining this question, I recalled hearing years ago that both chemicals -- Helium and Hydrogen possess enough energy to escape the atmosphere.
A couple of weeks ago, I wrote a blog post about cooking pasta like a chemist. The point of that post was to inspire people to imagine the dynamic environment that is occurring in the boiling water and the headspace just above it. While writing that post, I could not help but to return to the statement that I had heard several years earlier regarding both chemicals -- Helium and Hydrogen -- possessing enough energy to escape Earth's gravitational field. I started narrowing my curiosity down to the following question:
What properties enable the elements hydrogen and helium to escape the Earth's atmosphere?
Are these two chemicals special? Do other chemicals possess enough energy to escape Earth's gravitational field?
The answer is interesting but somewhat complex and still being researched. Below, I start to discuss the parameters which might give both of these chemicals the ability to act special (in the sense of escaping into space). Read on below to find out the answer.
Hydrogen & Helium Are Special!
As I found out, the process is simple yet complicated. How does that figure? Simple yet complicated? In order to understand the statement about these elements, we must take a divergent step for a brief backstory in chemistry. These two elements are gases at room temperature. In order to describe the behavior of the gases at a particular temperature, the "probability distribution" created by James Clerk Maxwell must be shown to illustrate our point. First, lets read the description of the "probability distribution" of molecular speeds devised by him taken from "Wikipedia":
In statistics the Maxwell–Boltzmann distribution is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann. It was first defined and used in physics (in particular in statistical mechanics) for describing particle speeds in idealized gases where the particles move freely inside a stationary container without interacting with one another, except for very brief collisions in which they exchange energy and momentum with each other or with their thermal environment. Particle in this context refers to gaseous particles (atoms or molecules), and the system of particles is assumed to have reached thermodynamic equilibrium.[1] While the distribution was first derived by Maxwell in 1860 on heuristic grounds,[2] Boltzmann later carried out significant investigations into the physical origins of this distribution.A particle speed probability distribution indicates which speeds are more likely: a particle will have a speed selected randomly from the distribution, and is more likely to be within one range of speeds than another. The distribution depends on the temperature of the system and the mass of the particle.[3] The Maxwell–Boltzmann distribution applies to the classical ideal gas, which is an idealization of real gases. In real gases, there are various effects (e.g., van der Waals interactions, vortical flow, relativistic speed limits, and quantum exchange interactions) that can make their speed distribution different from the Maxwell–Boltzmann form. However, rarefied gases at ordinary temperatures behave very nearly like an ideal gas and the Maxwell speed distribution is an excellent approximation for such gases. Thus, it forms the basis of the Kinetic theory of gases, which provides a simplified explanation of many fundamental gaseous properties, including pressure and diffusion.[4]
The distribution is very useful in describing the behavior of "ideal gases". In this context, helium is considered an "ideal gas" -- why you might ask? Because one of the properties of the helium molecule is "inertness". What does this mean? Typically, that helium does not react with other gases. On a side note, helium is very useful in carrying out chemical reactions that are "air sensitive." Helium gas is "inert" and serves the purpose of providing an "reactive" free environment in which desired chemicals can be introduced to carry out a chemical reaction. What do I mean by this? In the photograph below, there is a picture of a graduate student carrying out a chemical reaction in a "glove box" which is "air sensitive" -- the atmosphere in this case is Argon -- another "inert gas":
Using an environment of helium or nitrogen or argon is common in any chemistry department in the world.
What does this "probability distribution" look like?
Shown below is the general representation of Maxwell's Distribution of molecular/atomic Speeds:
Source: Pdbailey at English Wikipedia
As you can see, the distribution is greatly dependent on molecular weight. A heavier element like Xenon with a molecular mass of 131.293 grams/mole has a narrow range of speeds (0-500 m/s). Whereas the element Argon has a molecular mass of 40 grams/mole and a broader distribution (0-900 m/s). The lightest of the "Noble gases" is helium with a molecular mass of 4 grams/mole and a broad distribution (0-2500 m/s).
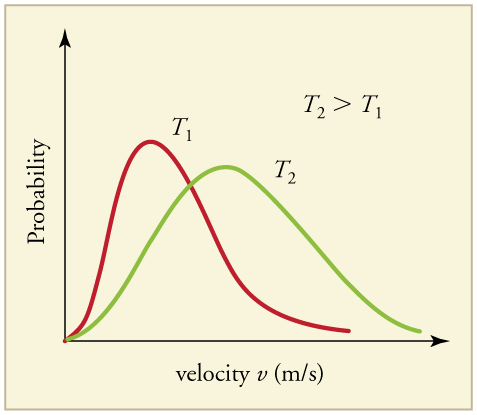
From this information, you should be able to compare the highest speed with that of the escape velocity needed to break the gravitational field from the previous calculations above for a space ship. Additionally, the other variable that determines the shape and location (i.e., the speed) is the temperature. After a brief search "online" I was able to find a good representation of the "probability distribution" dependency on temperature. For a given gas at two different temperatures, "OpenStax" has a great diagram shown below:
Source: OpenStax
Notice how the average speed of the molecule changes along with the top speed (determined by the tail of the distribution length) shown in the colors red and green. At higher temperatures, the distribution gets broad and the top speed is much greater. This is important in understanding how the gases act in the upper atmosphere. Naturally, at this point, you are probably asking yourself, how high would the temperature have to be to eject (play a dominant role) in the escape velocity.
What about temperature?
In order to calculate the temperature needed to provide enough thermal energy to eject a molecule of helium or hydrogen, an expression is needed for the speed of molecules at a given temperature. For this, the analysis of the "probability distribution" (breaking down the nature of the distribution curves) yields a "root-mean-square" speed of the following form:
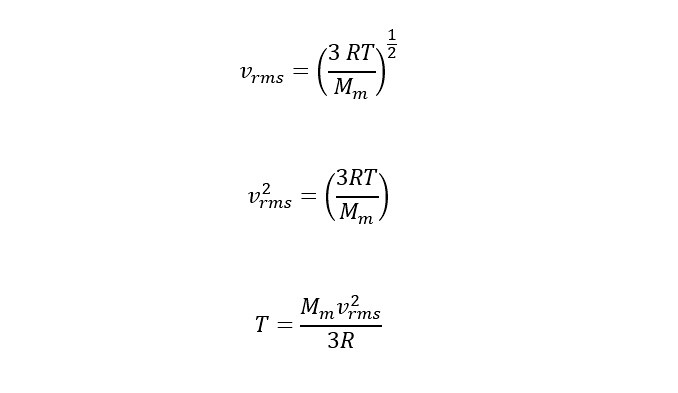
In order to calculate the temperature, the above expression needs to be rearranged to solve for temperature T as follows:
Plugging in the remaining values for the mass of the Earth, M, the "root-mean-square" speed, and the gas constant, R, yields the following:
That is hot! Does the atmospheric temperature ever reach the above temperature? Hopefully, not -- at least in the lower atmosphere. Further, the temperature does not reach this value along the distribution of height with temperature. Therefore, the only way to obtain enough energy to escape is through interacting in the complex upper atmosphere.
There are a number of factors along with the collisional energy that allow both molecules (hydrogen and helium) to escape. For the purposes of this post, we will focus on the dominant factor -- collision energy.
How does a person visualize this complexity within the atmosphere above them?
Look up into the sky. If the weather calls for a storm, then there will be clouds and just by inspection, the situation does not look good. Clouds help us visualize the complexity going on in the sky at any given moment. The shape gives us insight into the various patterns of wind moving around at various heights. Although, we are not able to perceive the depth of various patterns from the ground. Can we do better?
Sure, watch the weather channel with the satellite images. Shown below is a short video of a satellite image of a storm moving through the Southern California region. Watch how the storm moves across the region.
On the screen, the movement appears to be slow. But, if you had a sensor up in the sky, the situation might appear to be much more chaotic. Why is this realization important? Because, according the the explanation above based on the distribution of speeds of gases at a given temperature, even the lightest gases (hydrogen and helium) lack sufficient energy to overcome the barrier to escape the atmosphere. Naturally, this leads up to the following question:
Where does the remainder of the kinetic energy come from?
I was thinking about this while walking through campus over the last few days. Suddenly, I realized that the complexity in the atmosphere might easily be understood (visually) by looking at the state Lottery. Yes, the lottery. If you take a look at the short video (less than 30 seconds)below of the lottery drawing, you will see a container with balls that are being mixed quite rapidly.
If we were to remove the hype of the lottery and focus on the experiment (balls being mixed inside a container), then we should focus on the video below. Shown below is a video of just the "SmartPlay" lottery mixer:
As you can see, there is a large amount of kinetic energy in the system to begin with which is being supplied by the air to mix the balls in the container. When the time comes to draw a ball -- which is indicated by one ball being "ejected" up the center column and held by air to be read by the lottery announcer. The balls in the container could be compared to the atoms and molecules that are being mixed by the wind currents (in addition to the Earth's rotational energy contribution). The Earth rotates at a speed of around
The process of "ejecting" the ball could be analogous to a "chaotic current" in the upper atmosphere which would give the helium molecule enough energy to overcome the remainder of the barrier to the appropriate escape velocity of 7 miles/sec.
Formally, the bridge that connects Maxwell's Distribution of speeds with the escape velocity was introduced by a physicist named James Jeans. According to "Wikipedia," the mechanism of "Jeans escape" is a thermal contribution from the solar energy. Here is an excerpt:
One classical thermal escape mechanism is Jeans escape.[1] In a quantity of gas, the average velocity of a molecule is determined by temperature, but the velocity of individual molecules change as they collide with one another, gaining and losing kinetic energy. The variation in kinetic energy among the molecules is described by the Maxwell distribution.
The kinetic energy and mass of a molecule determine its velocity by E_{\mathit{kin}}=\frac{1}{2}mv^2.
Individual molecules in the high tail of the distribution may reach escape velocity, at a level in the atmosphere where the mean free path is comparable to the scale height, and leave the atmosphere.
The more massive the molecule of a gas is, the lower the average velocity of molecules of that gas at a given temperature, and the less likely it is that any of them reach escape velocity.
This is why hydrogen escapes from an atmosphere more easily than carbon dioxide. Also, if the planet has a higher mass, the escape velocity is greater, and fewer particles will escape. This is why the gas giant planets still retain significant amounts of hydrogen and helium, which have largely escaped from Earth's atmosphere. The distance a planet orbits from a star also plays a part; a close planet has a hotter atmosphere, with a range of velocities shifted into the higher end of the distribution, hence, a greater likelihood of escape. A distant body has a cooler atmosphere, with a range of lower velocities, and less chance of escape. This helps Titan, which is small compared to Earth but further from the Sun, retain its atmosphere.
An atmosphere with a high enough pressure and temperature can undergo a different escape mechanism - "hydrodynamic escape". In this situation the atmosphere simply flows off like a wind into space, due to pressure gradients initiated by thermal energy deposition. Here it is possible to lose heavier molecules that would not normally be lost. Hydrodynamic escape has been observed for exoplanets close-to their host star, including several hot Jupiters (HD 209458b, HD 189733b) and a hot Neptune (GJ 436b).
Interestingly enough, the variation of the speeds in the Maxwell distribution are similar to the deficit of Professor Jeans idea regarding the loss of gases to space. According to measurements made after he passed, the escape mechanism (based on thermal energy) cannot account for all of the gas that has escaped the orbit. Therefore, we are left with other mechanisms at play that contribute energy -- known and others that are unknown (i.e. still being researched).
As I mentioned at the beginning of the section regarding the elements hydrogen and helium, the dynamics are complex. Amazingly enough, contributions from insightful physicists such as James Clerk Maxwell and James Jean have withstood the test of time and held up as a significant contribution to evaluating molecular speeds based on temperature, molecular mass, and gravitational pull. How the gravitational system contributes to the escape of the distribution (the tail of the distribution without sufficient energy to obtain escape velocities) remains to be discovered?
Conclusion...
The dynamics are complex in the atmosphere above us. I say that not as an excuse, but a challenge to conquer them in the future. Find out what types of collisional energy contribute the escape velocity of a hydrogen atom. Why do other "heavier" molecules escape sometimes? How do other collisional exchanges contribute -- Rotational energy, Translational energy, etc.? How does the Earth's rotation contribute to the escape velocity of these small molecular systems?
One take-away message is concrete among many uncertain. That is, our ability to send a manned space shuttle into space without problems of breaking the gravitational pull is absolutely amazing. Our technological development has led us to understand the atmosphere to a large extent. As you can see, there is still a lot of room to grow intellectually. This is where each of us come in. We need to continue to opt for funding for space programs. As I will discuss in future posts, many technological developments are created as a result of such research. Until then, keep on learning as much as you possibly can about the world. Have a great weekend.


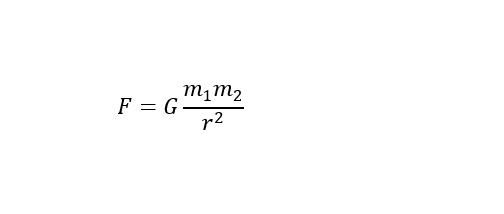
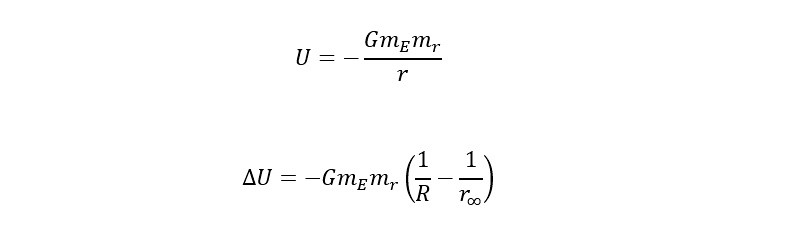
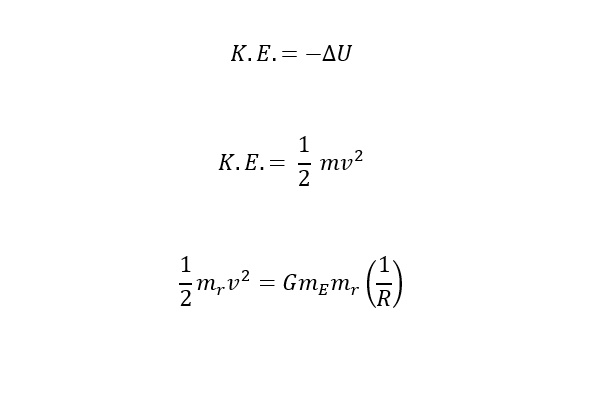
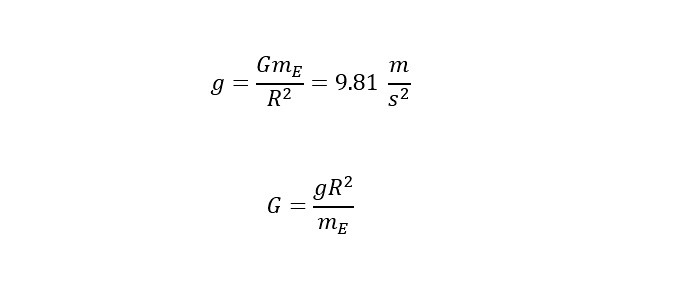
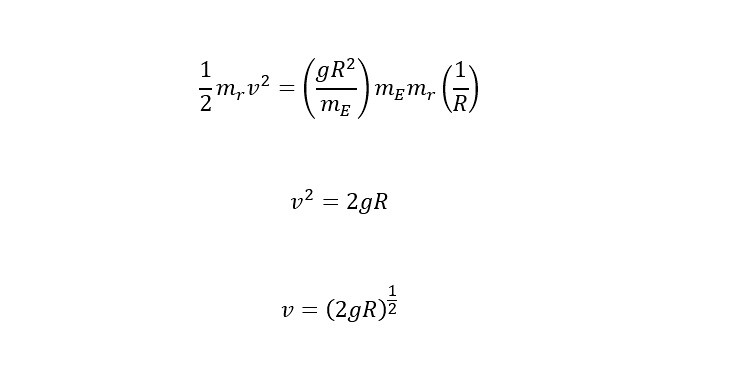



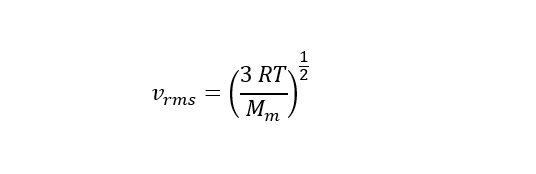

No comments:
Post a Comment