How much is a kiloton of Energy?
Regardless of what type of weapon was actually set off, I thought that an exploration into the amount of energy contained with a 'kiloton' of energy would be interesting. Over the decades, several reports of the threats of nuclear weapons have occupied news reports. I wonder how connected the public is with the threat of a given nuclear weapon. Part of the disconnect (I believe) stems from a lack of understanding of the energy contained within a weapon.
I thought that I would start with a 'small size' nuclear weapons that is on the order of 'kilotons' of energy. As described above, the news reported a distinguishing value of 13,000 tons of TNT. The value of 13,000 tons is referred to as '13 kiloton' -- which is equivalent since the prefix "kilo-' is a thousand. A 'kiloton' of energy can be defined from 'Wikipedia' as the amount of energy released in an explosion of a ton of TNT:
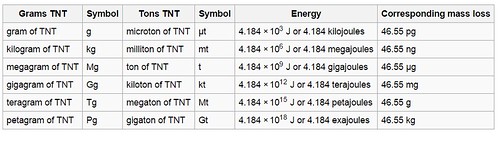
TNT equivalent is a method of quantifying the energy released in explosions. The "ton of TNT" is a unit of energy equal to 4.184 gigajoules,[1]which is approximately the amount of energy released in the detonation of a metric ton (1,000 kilograms or 1 megagram) of TNT. The "megaton of TNT" is a unit of energy equal to 4.184 petajoules.[2]
Additionally, in the 'Wikipedia' article for 'Kiloton' a table with conversion is given that shows how many Joules of energy are equivalent to a ton of TNT. Here is an image of the table 'borrowed' from 'Wikipedia' shown below:
How does one makes sense of the values reported in the table above relating the tons of TNT to Joules?
I could find objects or quantities and compare the power or energy needed to operate them to the value of 13 kilotons. Lets see -- below.
How does 13 kilotons compare in magnitude to other values of energy?
In order to understand the amount of energy, I will use 'dimensional analysis' to compare the amount of energy to three quantities: (1) Annual power consumption in Los Angeles County, (2) Amount of miles powering a Nissan 'Leaf' (2016 Electric Vehicle), and (3) Amount of time that can power a ceiling fan.
Starting off, I will ask the following question:
How does a 'kiloton' of energy compare to the amount of energy required to power the county of Los Angeles for an entire year?
In order to answer the above question, the amount of power required to run Los Angeles County would have to be known. Where does one find the amount of power required to run Los Angeles County in a given year? The answer is the "Electricity Consumption Data Management System." Upon choosing a year and county -- in this case "Los Angeles" and "2014" -- the amount is given in 69,997 million kWh. Or just say, 69.997 billion kiloWatt-hours.
What is the conversion of 'kiloWatt-hour' to Joules? Both quantities need to be expressed in the same units -- Joules or J. In order to convert to different units, the relation of the Joule to the 'kiloWatt-hour' is needed. There are many reference books with conversion tables available online. I like to resort to the easiest route first.
A kiloWatt-hour is defined by 'Wikipedia' as:
The kilowatt hour (symbol kWh, kW·h, or kW h) is a derived unit of energy equal to 3.6 megajoules.[1][2] If the energy is being transmitted or used at a constant rate (power) over a period of time, the total energy in kilowatt-hours is the product of the power in kilowatts and the time in hours. The kilowatt-hour is commonly used as a billing unit for energy delivered to consumers by electric utilities.
Converting a kiloWatt-hour to Joules of energy -- the power required for an hour is shown below:
But wait, where did the "3600 s" come from? Here is the conversion of an hour to seconds:
With a conversion factor in hand to convert from a 'kiloWatt-hour' to a Joule, I can start to determine the comparison of the annual power consumption of Los Angeles County to the energy contained in a 13 kiloton nuclear weapon. To start
In the first line, I took the annual power consumption of Los Angeles County (expressed in billions of kiloWatt-hours) and converted that to kiloWatt-hours per hour. Next, I calculated the number of Joules per hour that are equivalent to kiloWatt-hour per hour -- in order to do a direct comparison (same units of Joule).
With both quantities expressed in Joules, a direct comparison can be made and the number of hours can be determined as shown below:
A direct comparison shows that a 13 kiloton nuclear weapon would power the entire county of Los Angeles for just under 2 hours -- WOW! On one hand, that shows that a nuclear weapon has a tremendous amount of power. Whereas, on the other hand, the annual power consumption of Los Angeles county is enormous. No wonder the news is occupied by stories urging residents to try to save any amount of power possible on a daily basis.
One of the major concerns with the nuclear tests that were conducted by the North Koreans was centered around the possibility of testing a 'Hydrogen bomb' rather than a conventional atomic bomb. The difference in explosive power is supposedly enormous. In an article in the Journal 'Nature' titled "What Kind Of Bomb Did North Korea Detonate?", a better understanding of the difference in magnitude between the two types of bombs is explained. Here is an excerpt from the article:
A hydrogen bomb would have created a blast hundreds or thousands of times more explosive. In this kind of bomb, energy released from a fission-based device is used to trigger a separate secondary nuclear fusion reaction, in which hydrogen isotopes fuse together, typically releasing energy equivalent to megatonnes of TNT.
To differentiate between the type of bomb released or tested by North Korea, scientists from Korea were collecting data from seismic activity -- a good indicator. The current test revealed an activity of around 4.5 -- not indicative of a 'Hydrogen bomb.'
Knowing the difference between bombs is around 3 orders of magnitude, I can recalculate using the magnitude of a 'Hydrogen bomb' -- i.e., megaton -- which is shown below:
Wow!!! That is different. Another way to compare the two values is to inspect the 'exponents' of the numbers in question. In the case above, the two values of energy differ by two 'orders of magnitude'. Which is to say, without performing the calculation, I could have just guessed that the difference would be around 2 orders of magnitude different. I would not have been that far off. These calculations show the power of exponents. By inspecting the magnitude of the exponent, a good guess or approximation can be made.
Reality Check: Evaluating numbers is not as bad as you (the reader) might have thought!!!!!
How about a 2016 Nissan leaf -- how many miles can a person drive on 13 kilotons worth of energy?
To carry out the calculation, the number of 'kiloWatt-hours' for a fully charged battery must be obtained. I found a number -- 30 kiloWatt-hour -- which will supply enough power to drive around 150 miles. As noted above, in order to make a direct comparison of energy, all values must be expressed in the same units. Therefore, I will first convert the power to operate an electric vehicle (in this case a Nissan leaf) for 150 miles -- which is equal to 30 kiloWatt-hours -- to Joule per mile. The conversion is shown below:
The calculated amount above is the amount of Joules needed to drive a Nissan leaf 150 miles. From the calculations above comparing the power consumption of Los Angeles county, a guess can be made just by inspecting the difference in exponents. Comparing a power of 13 to that of 5 will produce a LARGE number of miles. In order to make sense of a large number, I need a large distance...How about the distance around planet Earth?
Lets recast the above question to the following:
How many times would that power a Nissan Leaf to drive around planet Earth?
What is the distance around planet Earth? According to the website 'Universe Today,' the distance is equal to 24,901.55 miles. With a distance in hand, the same comparison (and calculation) from above can be carried out which is shown below:
Oh my goodness. Now the energy contained within a 13 kiloton nuclear weapon seams large. So does the amount of power consumed on an annual basis by the entire county of Los Angeles. Wow.
Last but not least, I could not leave without choosing an appliance that a majority of people can relate to. I mean, if you do not live in Los Angeles county or have never visited, then the first calculation might be difficult for you to grasp. Alternately, if you do not have an electric vehicle or do not know anyone who owns one, the second calculation might be meaningless to you as well. Plus, electric vehicles are supposed to be efficient -- which would lead us to expect a vehicle to get a 'great amount' of miles out of a given 'battery charge.'
How about a ceiling fan?
A ceiling fan is common here in US households. My ceiling fan is loud and keeps me awake when I have to resort to using the damn fan during the hot summers. Lets end this blog post by calculating how long a ceiling fan could run (be powered) for running solely off of 13 kilotons of energy? In order to compare values, the power to run a ceiling fan must be determined. How do we get that? Look on the internet....I found an answer provided by 'Duke Energy' on a website that lists a variety of home appliances in units of 'kWh/hour' or 'kWh/month'.
According to Duke Energy, the power needed to run a ceiling fan for one hour is 0.075 kWh. I followed the same procedure as above to determine how long the ceiling fan would run for off of 13 kilotons. Note: since we know that the electric vehicle was able to circle the planet Earth nearly 3000 times, we can guess that the amount of time will be even larger in magnitude.
As a result, I chose to express the amount of time in years. Here are the calculations below:
Wow. As expected, the amount of time is extremely huge. A ceiling fan could be operated for 23,000 years off of 13 kilotons worth of energy. That is amazing. Have you realized yet that the amount of energy contained within a small nuclear weapon -- around 13 kilotons -- is actually a huge amount of energy?
Are we done here? I think so. Here is an assignment for you (the reader)....
Conclusion
Obviously, if you have read through the entire post above and worked through the calculations, the energy has been realized to be quite large. As a conclusion, I will keep the wording simple. I would challenge you to choose different quantities of energy and compare them to 13 kilotons by yourself. Leave the results in the 'comments' section below. And last but not least, have fun. I hope that in the future you will look at the concept and reporting of a nuclear weapon in a completely different light. Have a good night!
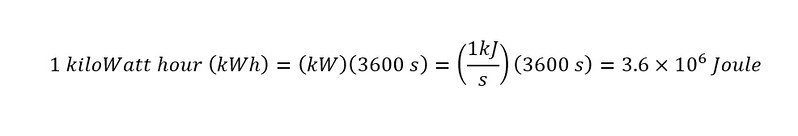
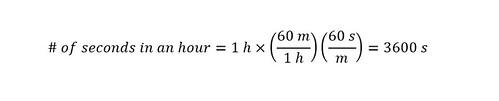
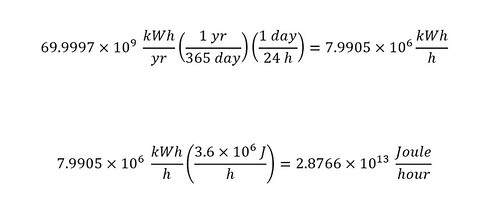

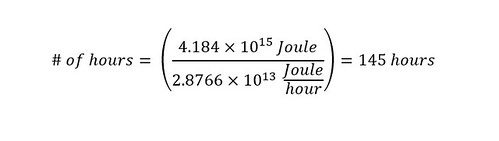



No comments:
Post a Comment