EARTH is poorly named. The ocean covers almost three-quarters of the planet. It is divided into five basins: the Pacific, the Atlantic, the Indian, the Arctic and the Southern oceans. Were all the planet’s water placed over the United States, it would form a column of liquid 132km tall. The ocean provides 3bn people with almost a fifth of their protein (making fish a bigger source of the stuff than beef). Fishing and aquaculture assure the livelihoods of one in ten of the world’s people. Climate and weather systems depend on the temperature patterns of the ocean and its interactions with the atmosphere. If anything ought to be too big to fail, it is the ocean.
Did you catch that statistic? Which one right? I am speaking about the sentence above stating that if all of the water on the planet was placed over the United States, a column would be formed that would have a height of 132 kilometers -- WOW. Upon reading this statistic, I could not help but wonder how many molecules of water are contained in such an enormous volume. Since the molecular scale is extremely small, chemists use a 'counting number' analogous to a 'dozen' (a dozen contains 12). What do I mean by this? In the following post, I will show how a chemist (myself) views the cited statistic through dimensional analysis. This includes varying scales and large numbers.
Molecules and Avogadro's Number
Chemists work with large amounts of chemicals. Not all chemists do. But on the scale of the bench top large amounts of chemicals are mixed. How do I know this to be true? Well, lets use a molecule that is ubiquitous to our world, but essential to our survival -- water. Water is composed of 'water molecules'. A typical water molecule is around 2.75 Angstroms. An Angstrom is 10 billionth of a meter.
If you were to line 4 million water molecules, the total distance would be a millimeter -- WOW.
Remember that in a single centimeter, there are 10 millimeters. This gives us a sense of the scale of a single water molecule. Although the blog post is concerned with the volume of water, therefore, putting the water molecules into 3 dimensional space might be of use. To start with, lets ask the following question: How many water molecules are in a single cup of water? A single cup of water is shown below in a measuring cup:
Source: Dreamstime
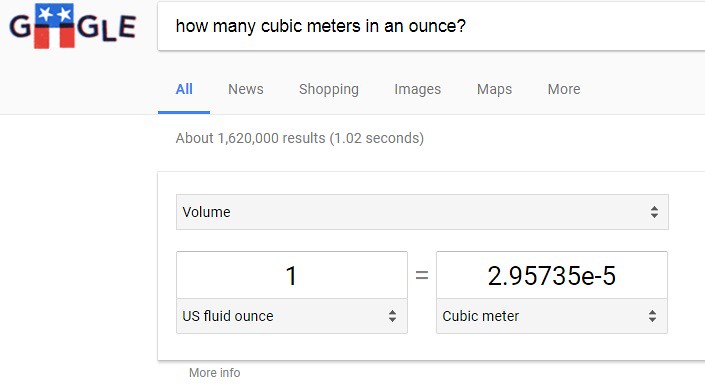
A cup has the volume of 16 ounces. In order to calculate the number of water molecules, a conversion must be made to change units from "ounces" to units of "cubic meters" - which will become apparent why shortly. First, type into a search engine like Google.com the following question: How many cubic meters are in an ounce? The following image appears shown below:
In a single ounce, there are 0.0000295735 cubic meters. To convert one cup of water (16 ounces) to cubic meters, the following conversion must be accomplished to yield cubic meters:
Right about now, you may be wondering why the conversion from units of "ounces" to units of "cubic meters" is necessary? To determine the amount of water molecules in a cup of water, the volume must be known along with density. Density is the amount of a substance in a given volume. The equation for density is shown below:
This equation is true for any substance (chemical). For water, the density at standard temperature and pressure is shown below:
The density of water at room temperature and pressure is 1000 kilograms per cubic meters. Now the previous requirement of expressing the volume of water in units of "cubic meters" should be apparent. Upon rearranging the equation for density to solve for mass, the equation appears as follows:
Since the volume is known from the conversion above along with the density of water, the mass of the water in a single cup can be calculated as shown below:
A single cup of water weighs 0.47 kilograms. For those of us who do not think in terms of kilograms, a conversion to grams is shown below:
A single cup of water weighs just over a pound (1 pound = 454 grams).
The amount of water (weight) which are contained in a unit of a "mole" is referred to as the "molar mass". If we look to "Wikipedia" for a definition of 'Molar Mass' we get the following:
In chemistry, the molar mass M is a physical property defined as the mass of a given substance (chemical element or chemical compound) divided by the amount of substance.
The "amount" of substance is the unit "mole". This unit is analogous to a "dozen" or a "case" -- meaning that "there are 12 eggs in a dozen" or "24 soda cans in a 'case of soda'". From the statements about the size and scale of the water molecule, a 'unit' is needed to express large numbers of molecules or atoms when discussing chemical reactions. That number is referred to as "Avogadro' number" and is defined from "Wikipedia" as:
In chemistry and physics, the Avogadro constant (named after the scientist Amedeo Avogadro) is the number of constituent particles, usually atoms or molecules, that are contained in the amount of substance given by one mole. Thus, it is the proportionality factor that relates the molar mass of a compound to the mass of a sample. Avogadro's constant, often designated with the symbol NA or L, has the value 6.022140857(74)×10^23 mol−1[1] in the International System of Units (SI).[2][3]
In the excerpt above, the constant Avogadro's number is properly expressed as follows:
Lets return to the calculation of the amount of water molecules in a single cup of water. The significance of Avogadro's number will become apparent once we arrive at an answer. With the total weight (mass) of the water expressed in units of 'grams' and the molar mass of water known (18 gram/mole), we can determine the number of moles in a single cup of water as follows:
Next, if the number of water molecules is to be determined (which it is), then using Avogadro's number, we arrive at the following final conversion:
The result display that in a single cup of water, there are "1.6 times ten raised to the 25th power" of molecules inside. How does that number look written out in long form? I show the number below:
From the long form of the calculated number of water molecules in a single cup above, the reader should be able to determine the usefulness of Avogadro's number. Imagine writing out these enormous numbers when discussing mixing two cups of chemicals. It makes little sense. Which is why, using Avogadro's number is extremely useful. Discussing mixing two glasses of water as mixing two amounts of 26 moles each is easier than writing out endless zeroes and commas.
The utility of Avogadro's number and the 'mole' should be apparent now. When discussing mixing large amounts of chemicals -- which is the case on the physical scale on which we live, the use of 'molar amounts' or 'moles' are extremely useful. Otherwise, our notebooks would be filled with countless numbers of zero's and comma's which would be both confusing and to lengthy.
The above calculation was for a single cup of water. Remember, that in the introduction the total amount of water for the entire planet was given. In the next section, through dimensional analysis the stated volume is cast into perspective with Avogadro's number and the unit of a 'mole.'
How Many Water Molecules Are In The Ocean (Planet)?
With the number of water molecules in a cup known, the next volume to cast into perspective is the total number of water molecules in all oceans on the planet. Using a similar methodology as the one above, the starting point will be to determine the total volume of water mentioned in the introductory excerpt. In the above excerpt, the total volume mentioned is a column of water with an area equivalent to the United States and a height of 132 kilometers.
An expression for the volume is shown below:
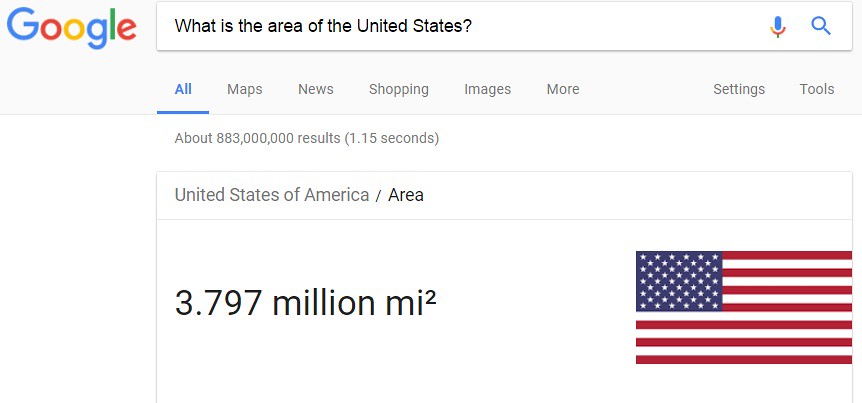
In the excerpt from the article above, the height is known -- 132 kilometers. To solve the equation for the total volume of water in all of the oceans on the planet, the area of the United States needs to be determined. If we ask "Google.com" the following question: What is the area of the United States? The following answer is shown below:
The total area of the United States is 3.797 million square miles. You should notice that the area of the United States is expressed in units of "square miles" whereas the height of the column of water is in units of "kilometers". In order to move forward in solving for the total volume of water, a unit conversion needs to be accomplished. The area of the U.S. needs to be converted from units of "square mile" to units of "square kilometer" as shown below:
With all of the units uniform (meaning expressed in the same unit), the total volume of water in all of the oceans on the planet can be solved as follows:
Using the same methodology as above for solving for the amount of water molecules in a cup, the equation for density can be rearranged to solve for mass as shown below:
Remember, the units of density were "kilograms per cubic meter" from above. Before the values can be plugged into the equation above, a unit check needs to be accomplished. The total volume of water which was calculated above is expressed in units of "cubic kilometers" -- which means that a unit conversion must be done to solve the expression for "mass" above. The conversion is shown below:
Now the units appear to be uniform. The density is expressed in units of "kilogram per cubic meter" and the volume is expressed in "cubic meters". With an expression for the mass of the water contained in all of the oceans, plugging in the values that have been obtained (through reference and calculation) the equation can now be solved as shown below:
The mass above represents the total weight of all of the water that is contained on the planet!! Next, using the 'molar mass' of water (i.e. mass of water contained in a mole of water) the amount of moles can be determined as follows:
In all fairness, we should expect to see a huge number -- an incomprehensible number. Why? Because in our earlier calculation, we determined that there were an enormous amount of water molecules contained in a single cup of water. Therefore, if there were 26 moles of water in a single cup of water, then the amount of water on the entire planet should be astronomical.
Remember, a mole is a 'counting number' which is useful for chemists since the size and scale of molecules are very small. Avogadro's number is stated again as:
The number of atoms or molecules in a mole is the same "6.02 times ten raised to the 23rd power". This is analogous to the fact that there are "12 eggs in a dozen eggs" or "24 cans of soda in a 'case of soda'" - there are Avogadro's number of atoms or molecules in a 'mole.'
When I first read the cited statistic above regarding the total amount of water in all of the oceans on the planet, I was curious to evaluate that amount of water in terms of 'moles' and compare that to Avogadro's number - which is to say:
Given the total number of moles of water on the planet, how does that number compare to Avogadro's number?
To answer the above question, we need to calculate the number of 'moles' of water -- which we already have. In order to evaluate that answer relative to Avogadro's number, we simply divide the two numbers as shown below:
The result indicates that the total number of moles of water is only 12% of Avogadro's number. That shows how large Avogadro's number is -- how astonishing the number is.
Conclusion...
In the paragraphs above, the cited statistic of an enormous volume of water has been cast into perspective. The perspective of a chemist. Furthermore, the volume is the total amount of water on the planet. That amount which seems astonishing large is only 12% of Avogadro's number when formulated into 'units' of 'moles'. The mole is an enormous number. Although, the size and scale of molecules are extremely small. With 4 million water molecules lined up which is equivalent to a single millimeter, we really get a sense of the size and scale which chemists who work in the field of 'nanotechnology' work at.
Last but not least, the above is an exercise to view the total amount of water in a completely different perspective - that of a scientist. In the future, when you pick up a cup of water, I hope that this blog inspires you to view the liquid inside in terms of water molecules. Try it and see. Take a look at the world from a completely (and sometimes uncomfortable) different view. Chemistry is not to be scared of, but appreciated. In order to think rationally about the world around us from the chemist's standpoint, we must know how a chemist views the world. The above is an introduction into my view of the world.
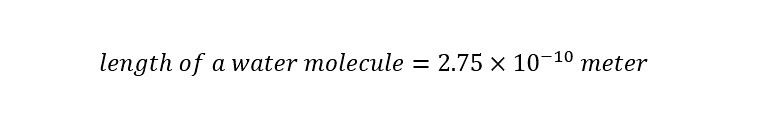
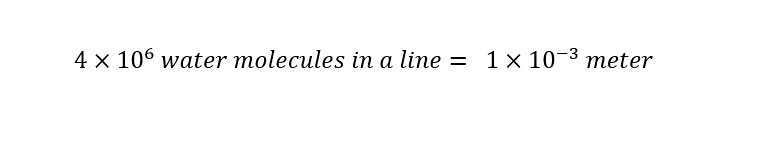

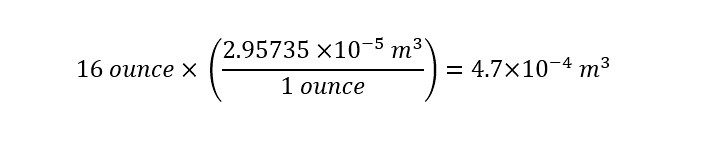

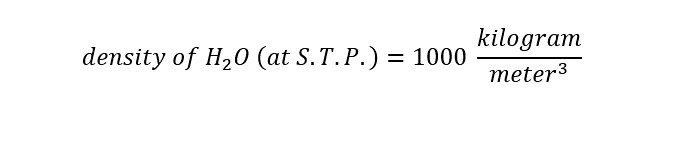
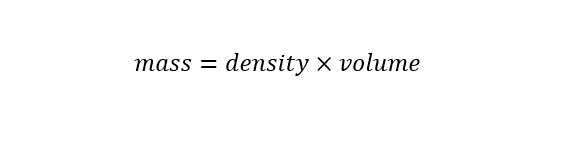
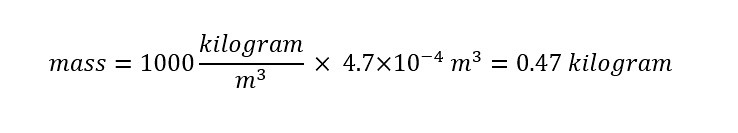

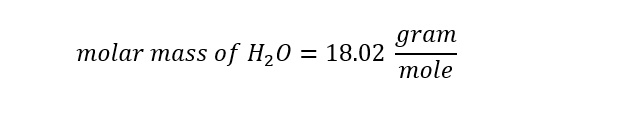
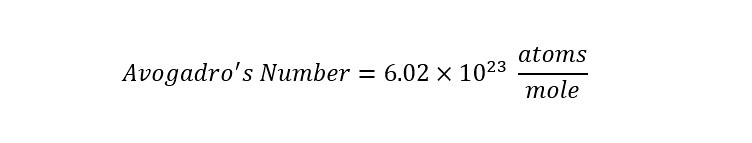
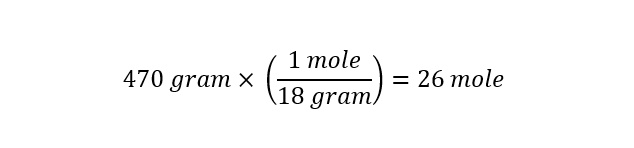
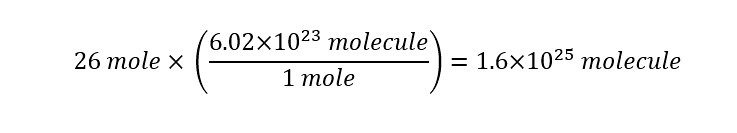
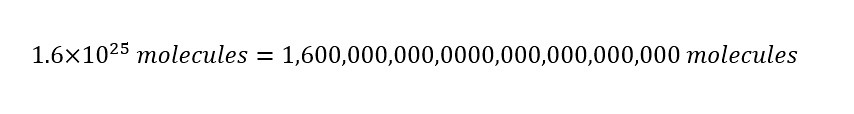
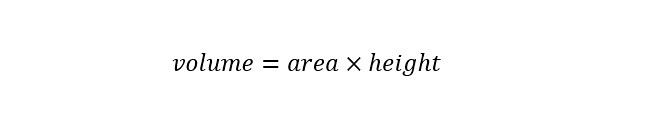
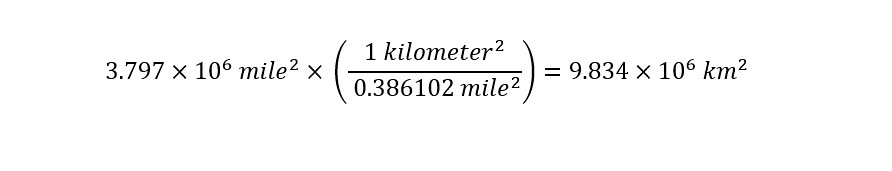
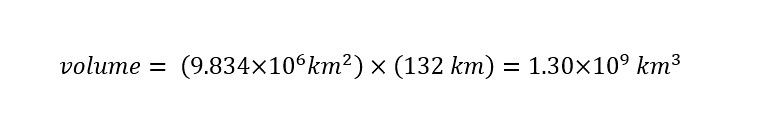

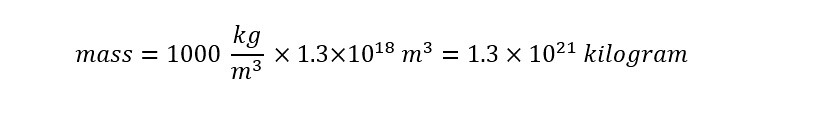
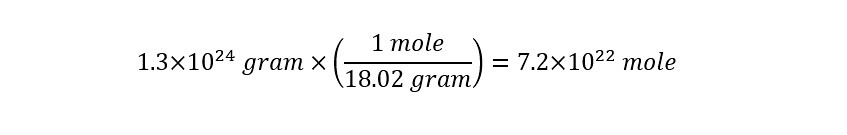
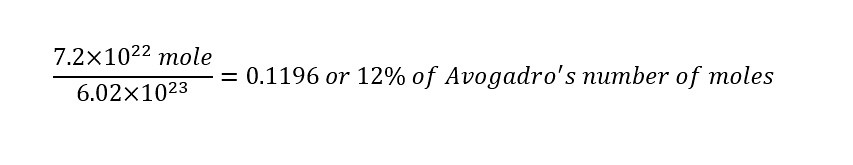
No comments:
Post a Comment