Wax Worms Eat Plastic?
A commonly held myth is that most discoveries are made by accident in science. Science research is a repetitive process of collecting data, interpreting data, and then repeating the process to validate the initial findings. Although, in a few instances, there are discoveries made by accident. In a recent on the website "Research Gate" titled "This plastic-eating caterpillar can help us get rid of our trash" an accidental discovery was made by a scientist tending to her bees:
The initial discovery was made not in a lab, but at the home of Federica Bertocchini, a researcher at the Spanish National Research Council. An amateur beekeeper, Bertocchini found a wax worm infestation in some of her beehives. “In cleaning the beehives, I put the worms in a plastic bag,” she explained. “After a short while, they had escaped, and the plastic bag was full of holes.”
After discovering the escaping worms, researchers went onto to discover that the worms digestive systems were breaking down polyethylene into ethylene glycol by breaking bonds. This led the researchers to further quantify the amount possible for a given wax worm to break down over a given time:
Other methods for breaking down polyethelene, which use corrosives like nitric acid or certain bacteria, take months to work. By contrast, 100 wax worms can biodegrade 92 milligrams of polyethylene in a mere 12 hours. “We do not know how wax worms developed this ability, but it might be that they evolved such a mechanism because they eat wax,” explains Bertocchini. “Wax and polyethylene have a similar chemical structure.”
The researchers have no plans to inject enormous quantities of wax worms into landfills anytime soon. Although, they are intensely interested in the chemistry behind the wax worms ability to break down plastic so easily. As is the case with a large part of science, nature holds the most efficient pathway for a given process. If any research could shed light on improving our ability to break down plastics by creating a better biodegradable plastic -- that would be great.
I was intrigued by the discovery and quantification of plastic which wax worms could process over a 12 hour period of time. 92 milligrams seems like a large amount for a wax worm. This led me to the following question -- the subject of the blog:
How many wax worms would be needed to break down 3.6 million tons of plastic each year?
Wax Worms Go To Work
In the question above, the amount of plastic is given which needs to be broken down in a year. To answer the question, we need to know the rate at which a single wax worm can process plastic. The article above gives a value of 92 milligrams/hour. There are two ways we can tackle the problem:
1) Figure out the amount of plastic each wax worm (at a rate of 92 milligrams per 12 hours) can eat in a year and follow that with multiplying that number to reach 3.6 million tons.
2) Start with rate of 3.6 million tons/year to figure out how many worms would be needed through a conversion process.
In this blog post, we will tackle the problem by method 2. To determine the number of worms needed to process (breakdown) 3.6 million tons of plastic in a given year, a unit conversion is necessary. The number cited (3.6 million ton) is expressed in units of 'ton'. The rate of plastic degradation of plastic by the wax worm per hour can be expressed as follows:
The researchers determined that within a period of 12 hours, each worm could process (breakdown) 92 milligrams of plastic. By dividing 92 milligrams/12 hours, the rate is now expressed as 7.7 milligrams/hour per worm. That is, each worm can process 7.7 milligrams of plastic within one hour. Next, the conversion of units of tons to milligrams needs to be carried out as shown below:
In the first line, the number of tons -- 3.6 million is expressed in scientific notation. The second line is the conversion of units from 'ton' to 'milligram' per year. After multiplying through the values above, the answer indicates that 3.6 million tons/year is equivalent to 3,300,000 - billion milligram/year -- WOW!
The rate of a single wax worm was given in units of 'milligram/hour'. Therefore, in order to use the two values, a second unit conversion is needed from 'mg/year' to 'mg/hour' as shown below:
Now, we can compare the rate in units of 'mg/(hour)(worm)' with units of 'mg/hour' to yield the number of worms. Understand? By dividing the total number of milligrams of plastic needed to be broken down by the rate at which each worm can eat will yield the total number of worms needed in a given year.
The results suggest that in order to process (breakdown) 3.6 million tons of plastic in a single year by using wax worms exclusively, a worm breeder would have to provide us with 4.1-billion wax worms.
Conclusion...
In the spaces above, I have shown how to calculate the number of wax worms needed to accomplish the job. I would be fascinated to see the other method displayed by a reader. Care to work that out and show me? Regardless, the number of wax worms needed is huge. I do wonder how many worms a breeder can breed at a single time? Furthermore, how much space would be needed to occupy 4.1 billion wax worms? These are questions which could be answered in the future. For now, each of us can rest assured that a calculation is accessible for determining the number of worms needed to eat 3.6 million tons worth of plastic.
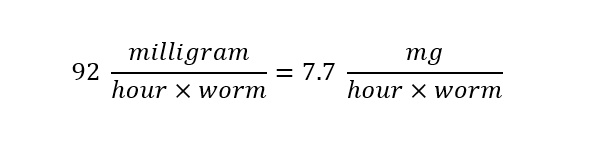

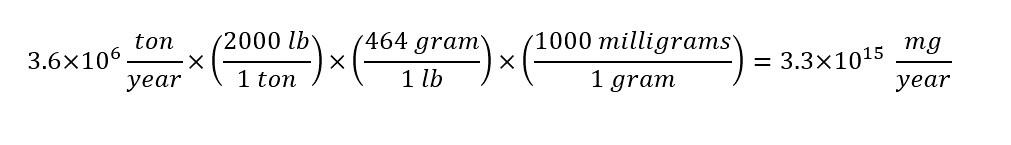

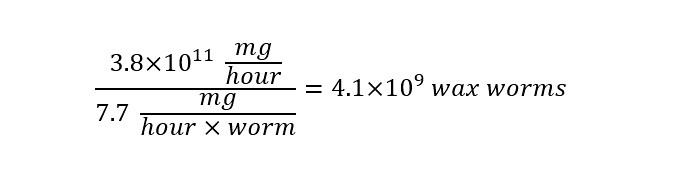
No comments:
Post a Comment