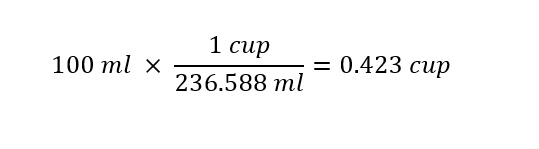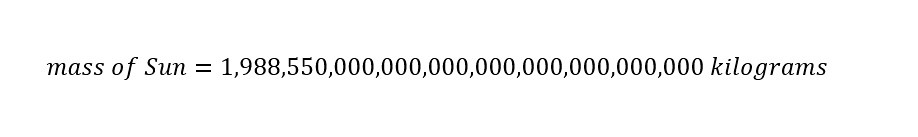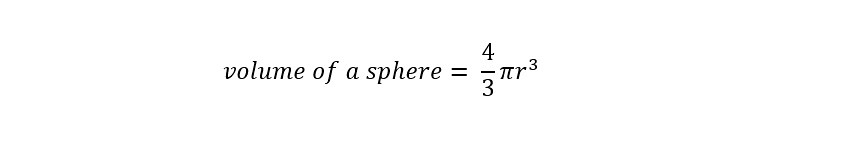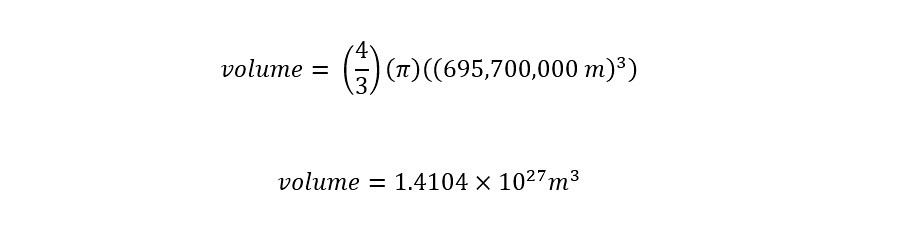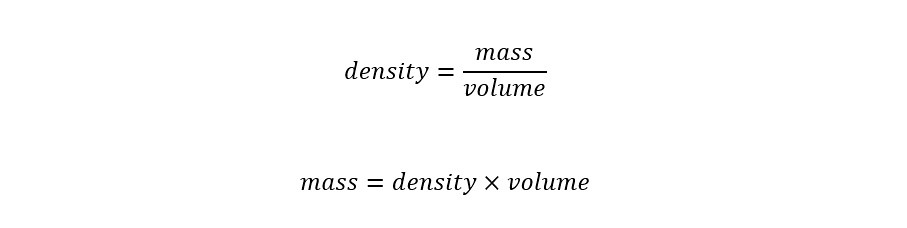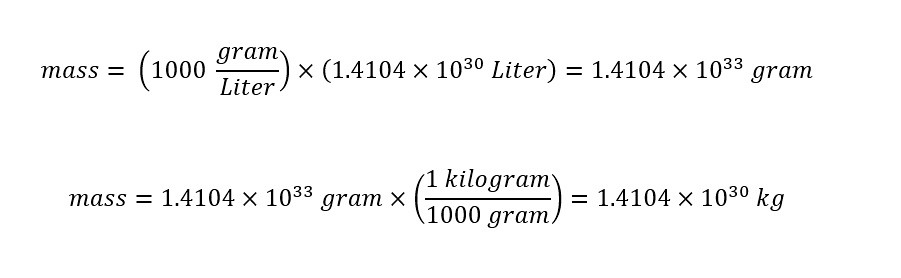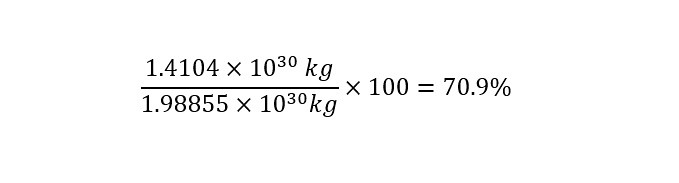What Is Dimensional Analysis?

Source: Singularity Hub

What is dimensional analysis?  Have you ever used dimensional analysis in your everyday life?  Here is the introductory description which is located on the Wikipedia page for "Dimensional Analysis":

In engineering and science, dimensional analysis is the analysis of the relationships between different physical quantities by identifying their base quantities (such as length, mass, time, and electric charge) and units of measure (such as miles vs. kilometers, or pounds vs. kilograms vs. grams) and tracking these dimensions as calculations or comparisons are performed. Converting from one dimensional unit to another is often somewhat complex. Dimensional analysis, or more specifically the factor-label method, also known as the unit-factor method, is a widely used technique for such conversions using the rules of algebra.[1][2][3]

The concept of physical dimension was introduced by Joseph Fourier in 1822.[4] Physical quantities that are of the same kind (also called commensurable) have the same dimension (length, time, mass) and can be directly compared to each other, even if they are originally expressed in differing units of measure (such as inches and meters, or pounds and newtons). If physical quantities have different dimensions (such as length vs. mass), they cannot be expressed in terms of similar units and cannot be compared in quantity (also called incommensurable). For example, asking whether a kilogram is greater than, equal to, or less than an hour is meaningless.

Any physically meaningful equation (and likewise any inequality and inequation) will have the same dimensions on its left and right sides, a property known as dimensional homogeneity. Checking for dimensional homogeneity is a common application of dimensional analysis, serving as a plausibility check on derived equations and computations. It also serves as a guide and constraint in deriving equations that may describe a physical system in the absence of a more rigorous derivation.

Wow!  Does that sound complicated?  Basically, what the description says above is that if you are comparing the mass of two oranges, both the units of measurement (weight) in this case have to be in the same 'units' - grams, pounds, kilograms, etc.  If you weight orange number #1 and report a weight of 70 grams, then try to compare a second orange's weight reported as 0.400 kg (kilograms) - then the comparison cannot be completed.



At least until you convert the weight of orange #1 to units of kilograms or weight #2 to units of grams.  If both weights were expressed in the same units -- say grams, then orange #1 weighing = 70 grams -- would be much smaller than orange #1 weighing = 400 grams.  The same logic applies to base quantities (dimensions) -- like length, mass, volume, height, speed, etc.



How about trying another route to clarify the description in the excerpt above.  If you have ever tried to follow a recipe while cooking, then chances are you have engaged in 'dimensional analysis' without knowing that you were doing so.  Don't believe me? Follow the quick cooking example below.

Example: Cooking

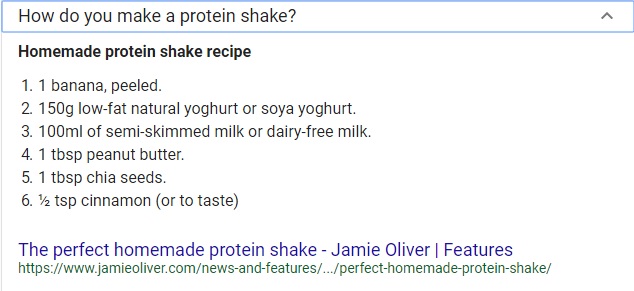
Here is a quick example of using 'dimensional analysis' in your kitchen.  Take the recipe shown below as an example:

The recipe above calls for 100 mL of milk.  That is 100 milliliters of milk.   What if the kitchen in which you are preparing the shake does not contain a 'measuring cup' shown below which is extremely useful in converting between different units of measurement:

Source: HomeDepot

Upon closer inspection of the image of a 'measuring cup' above, one can easily see a series of markings at different heights with different labels.  These labels indicate different volumes of measurement in different units.  According to the image of the recipe shown earlier, the amount of milk called for in creating the shake was 100 mL -- Which could easily be converted using the instrument above -- i.e. measuring cup.



Although, what would you do if you did not have a measuring cup within the kitchen in which preparation of the shake was taking place?  How would a person find the conversion factor to convert between units of 'milliliters' and units of 'cups'?  One easy method with the advent of the internet has been to resort to to a 'search engine' like 'Google' or 'Bing'.



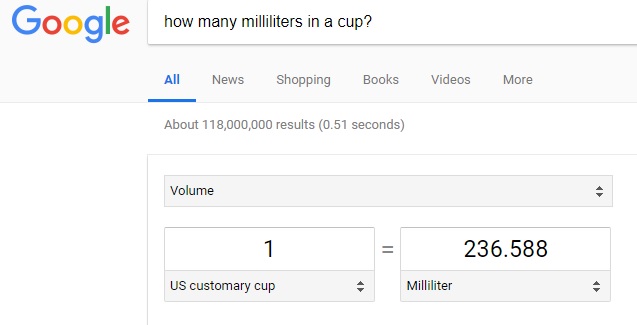
Proceed to bring up a web browser and bring up Google.com and type in the search space: "How Many Milliliters In A Cup?" and the web page with the conversion (interactive) columns should appear as shown below:

Note: The conversion shown above is 'interactive' - which means that the labels are 'drop down' menus which can serve to change either 'units of measurement' or 'dimensions' (i.e. length, area, volume, time, speed, etc.).  Feel free to play with the web page to convert between units of various dimensions.



Next, with the conversion factor known which will assist us in converting between units of 'cups' and units of 'milliliters', the remaining step in the conversion is to carryout a mathematical operation as shown below:

The result indicates that in order to follow the recipe (approximately -- not precisely), roughly 1/2 cup of milk will correspond to 100 milliliters of milk.  Note that the conversion is approximate -- since 1/2 = 0.5 not 1/2 = 0.423 !!!



Is the method of carrying out a dimensional analysis problem is clear?  If the answer is yes, then you are ready to read past blog posts which mainly use 'dimensional analysis' to cast statistics reported in the news into perspective -- click here to access the index of past blog posts.  If you are not comfortable with carrying out 'dimensional analysis' problems, see the tutorial below.

Dimensional Analysis Tutorial

A Tutorial on Dimensional Analysis is shown below:

After watching the video above along with reading the content of the blog post so far, you may be wondering where to get conversion values if not from the internet.  Science textbooks have conversion tables.  After a quick search of conversion tables, the 'Accidental Scientist' appeared with a host of information.  Here is a screenshot of an example of a table of conversions below.  Note: if you click on the source, you will be directed to the site:

As you can see, there is no need to memorize conversions -- at least all of the conversions.  That is what reference materials are for when needed.

Conclusion...

In the paragraphs above, the useful (and fun) method of carrying out calculations using 'dimensional analysis' was shown.  Armed with the power to carry out comparisons with conversion factors allows you to verify a large portion of statistics which are reported in the popular news on a day-to-day basis.  Is this useful?  Depends on how much energy that you choose to exert in understanding the process of using it to live a better life.


Understanding the power of comparison with conversion factors will add extra dimensions of happiness to your life.  How do I know?  When a person can visualize or comprehend the magnitude of a reported statistic by putting the value into perspective using dimensional analysis, the problem or subject matter of the news article becomes that much more useful to the reader.  Again, thank you for visiting the website and check out the dimensional analysis blog posts by clicking here.



Related Blog Index:


Dimensional Analysis Of Statistics And Large Numbers - Index Of Blog Posts

How Much Would The Sun Weigh If Filled With Water?

Recently, I was listening to a radio show called "StarTalk" with the physicist Prof. Neil deGrass Tyson.  The episode was a panel of astrophysicists talking about the study of 'black holes' in our universe -- which was completely fascinating I might add.  During the discussion, there was a large amount of dimensional analysis going on in order to drive home the relevance and complexity associated with studying 'black holes' from Earth.  One statistic popped up out of nowhere:



If the Sun was filled with water, it would weigh nearly as much as it does now!



At the time, I was riding the train back home from vacation and did not have my laptop handy to look up a few values to explore the stated statistic further.  Since then, the statement has been lingering in the back of my head.  Today, I decided to perform a couple of calculations to either verify or debunk that statement.  Below are the result of those calculations.

How Much Does The Sun Weigh?

In order to tackle such a calculation, a few values need to be known.  First, the weight of the Sun needs to be obtained.  If the weight of the Sun is not known, then a comparison based on an analysis is useless.  Second, the Sun will be approximated as a perfect sphere for calculation purposes.  Third, since the sphere is going to be used as the shape of the Sun, then a formula for the volume needs to be obtained.  Finally, the density of water needs to be known to use as a correlation factor of volume to weight.  Right about now you are probably thinking the following:



How do all of these values and formula come together to confirm the statement above?



I will show you in the paragraphs below.  In order fully grasp the nature of the analysis that is about to unfold, lets cast the Sun into a better perspective.  The weight of the Sun can be obtained from the resourceful "wikipedia" page along with other useful facts such as the description shown below:

The Sun is the star at the center of the Solar System. It is a nearly perfect sphere of hot plasma,[13][14] with internal convective motion that generates a magnetic field via a dynamo process.[15] It is by far the most important source of energy for life on Earth. Its diameter is about 109 times that of Earth, and its mass is about 330,000 times that of Earth, accounting for about 99.86% of the total mass of the Solar System.[16] About three quarters of the Sun's mass consists of hydrogen (~73%); the rest is mostly helium (~25%), with much smaller quantities of heavier elements, including oxygen, carbon, neon, and iron.[17]

Wow!  The description above sets the tone for the following analysis. First, the numbers involved are going to be VERY large (many zeroes before the decimal place).   The Sun is enormous and dwarfs the Earth easily in its description.  The weight of the Sun is listed on the 'wikipedia' page as the following:

The mass of the Sun above is expressed in 'Scientific Notation' to abbreviate the enormous number.  Typically, scientist use this 'abbreviated notation' to express huge numbers more easily.  At the same time, scientific notation can also be used to express very small numbers (i.e., a billionth of a meter, a nanometer = 1/1,000,000,000 meter).  If the mass of the Sun expressed in scientific notation was written out in long form, the mass would appear as shown below:

Alright.  After viewing the mass of the Sun in long form, the ease of using 'Scientific Notation' is completely understandable.



To start the calculation, the volume of a sphere needs to be known.  Below is the volume of a sphere in equation form:

In order to calculate the weight of the Sun filled with water the following steps need to be taken:


1) Obtain the radius (denoted as 'r') of the Sun


2) Calculate the volume of the Sun


3) Calculate the mass of the Sun from the volume (with the density of water)


4) Compare the calculated mass of the Sun to the stated mass (above) from 'wikipedia'



The steps are quite simple.  Keep in mind though, that in order to compare or calculate values, wthe values need to be in correct 'units' (i.e., 'kilogram,' 'gram,' 'milliLiter,' 'Liter,' or 'cubic meters').  Otherwise, completing calculations and comparing calculated volumes is impossible -- like 'comparing apples with oranges.'



With this in mind, lets start calculating the mass of the Sun filled with water following the steps above.  First, the radius of the Sun needs to be known.  From the 'wikipedia' page, the radius of the Sun is stated to be either 695,700 kilometers or 109 times the radius of the Earth.  Expressed  in long form for the calculation, the radius of the Sun is shown below:

The radius of the Sun can be directly plugged into the equation for the volume of a sphere above to yield the following:

The volume of the Sun is shown above.  In order to calculate the mass from the volume, we need the density of water.  Density is the amount of mass contained in a given volume.  For water, the value of the density is 1.00 gram/milliLiter.  Since there are 1000 milliLiters in a single Liter, then the density for water can be expressed as 1000 gram/Liter.



The expression for density of a given molecular compound can be expressed as the 'mass' per 'volume' as shown below:

The first line shows the equation for the density of a given molecular compound.  In the second line, the equation is re-arranged to yield the 'mass' from the two parameters 'density' and 'volume'.  Plugging in the values from the calculation and reference (density) value, the 'mass' of the Sun can be calculated as shown below:

The calculated mass of the Sun is shown above.  Of course, the value of the mass is enormous as expected -- which is good.  Returning to the statement above -- which motivated the article:



If the Sun was filled with water, it would weigh nearly as much as it does now!



The following question can be asked regarding the calculated mass and the reference mass listed from 'wikipedia':



How do the two masses (theoretical and calculated) compare to each other?



The easiest way to compare two value (in the same units -- i.e. 'kilogram') is to express them as a ratio of each other as shown below:

The result shows that the two values have the same "order of magnitude" -- that is 10 raised to the power of 30.  But the two values are NOT nearly the same -- Why Not?   Read onto find out.

Plasma Is Denser Than Water

In carrying out the calculation above, there are a number of assumptions listed below:



1) The Sun is shaped as a sphere


2) Density of water at 25 degrees Celsius was used in the calculation



What was not figured in was that the density of an mass can change with temperature.  The Sun has a reaction going on in the core of the sphere.  There are four states of matter: Gas, Liquid, Solid, and Plasma.  In the calculation above, the state of matter used for water was a liquid -- 1.00 gram/milliLiter at 25 degrees Celsius.



According to the 'wikipedia' page for 'plasma,' the density can change significantly with temperature as shown in the image taken below:

Source: Jafet.vixle at English Wikipedia

What does this mean in the overall calculation?



Why should I (you -- the reader) care?



Understanding the accuracy of an approximation is crucial to the words that are used to describe the comparison of two values.  In the situation of comparing two masses -- the result of the calculation and the theoretical mass from 'wikipedia' -- you can easily see that the two are not comparable.  In order to understand the reason why that is the case or might be -- look toward the density of the molecule in question -- in this case water.



The density inside plasma can vary up to 7 orders of magnitude different from that in room temperature.  Meaning, you can pack more mass into a given space.

Conclusion...

The above calculation is a great opportunity to illustrate the methodology of carrying out a 'dimensional analysis' problem.  Based on the result of the calculation, the statement above regarding the mass of the Sun filled with water nearly being equal to that of the current weight is not necessarily true.  Although, the two values did have the same 'order of magnitude' -- 10 raised to the power of 30.



Nevertheless, the exercise was fun and displayed the power of 'dimensional analysis.'  Now, you have the ability to carry out the same calculations on your own.  The next time that you are listening to the radio or reading the paper and find an interesting fact, you can verify the two values on your own.



Until next time, Have a great day!