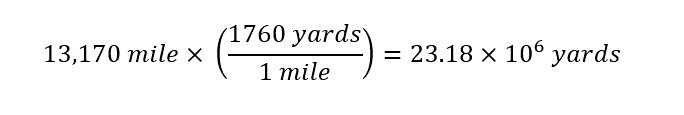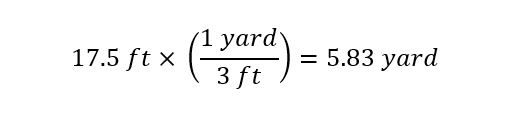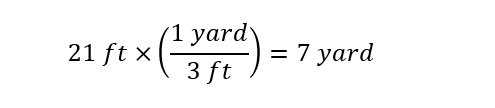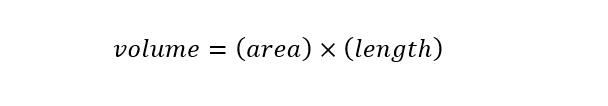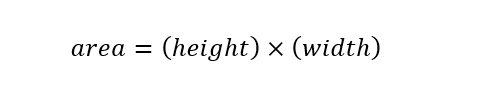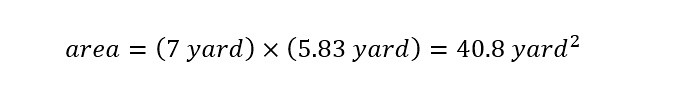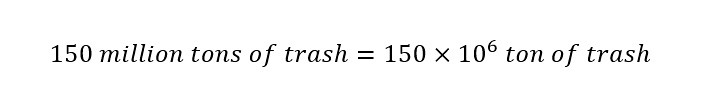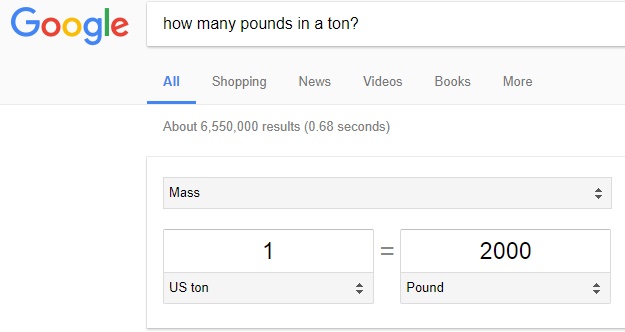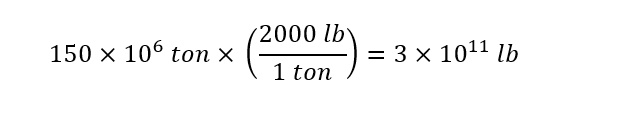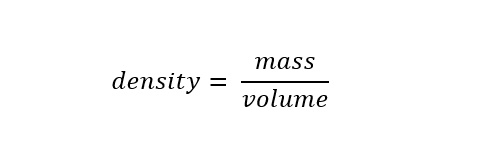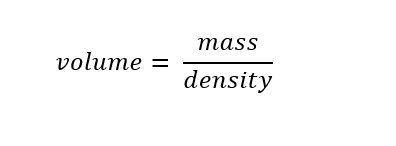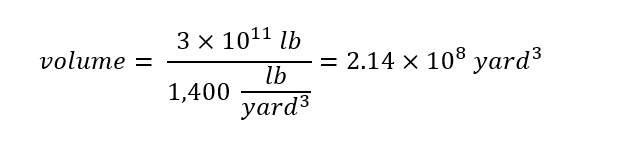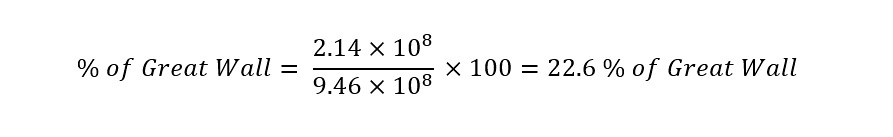A Virtual Tour Of A Human Cell?

With the leaps and bounds that technology has taken over the decades comes new fascinating ways of viewing science.  Yes, traditionally, these 'cool graphics' have been reserved mainly to the video game industry.  Now, a graduate student -- Tyler DeWitt has teamed up with Google and made a virtual tour of the human cell.  Yes, a grant had to be written to support the work.  What is amazing about the virtual tour is the clarity and visualization that is possible. The name Tyler DeWitt should be familiar to you (if you have kept up with the posts written on this site) -- you will remember him from a previous post of mine on communicating science.    Without further ado, here is an 8 minute tour of the cell shown below:

Was that not amazing?  I have been a proponent of virtual reality in teaching chemistry for quite a while.  Although, there remain a considerable amount of 'kinks' to be worked out until each student finds themselves in a 'virtual classroom.'  Videos like the tour above give us a glimpse into the possibilities of the future in teaching rather difficult concepts to students.



Furthermore, the concepts discussed in the video above tie in quite nicely with the mechanisms of disease from the medical community.  Imagine if the two were tied together to show a patient how a drug works?  Or if the mutation of a gene resulted in the formation of an incomplete protein?



A perfect example would be a visit to the doctor who uses the technology above in educating the patient.  If a doctor were to use the visualization above to convey that the drug a person was prescribed to was interacting with another active site, then educating the patient to change to a different medication might be much easier.  In the future, the role of virtual reality will only increase not decrease.



Examples like the video above inspire confidence in changing toward a more educated public regardless of the what concept is being conveyed.   As is often said..."a picture is worth a thousand words..."  Until next time, have a great day.


Related Blog Posts:


A Virtual Tour Of A Plant Cell? Really?

Subscribe And Receive 'Mike Thinks' Blog Posts Hot Off The Press!!

The other day while assisting undergraduate chemistry students (California State University at Northridge) of the Chemistry department develop their blog site, a new addition to this site came to mind.  One of them asked if I could set up a way to subscribe to their site in order to receive each post right off the press -- so to speak -- A.S.A.P. 



Obviously, this led me to the idea of adding that feature for those who are interested in receiving each post after I publish -- right to your e-mail 'inbox'.  If this is the case, then simply go to the front page (most recent post) and look toward the upper right hand side of the webpage.  There should be a blank space below the written words -- "Follow by E-mail = Get A New Post Delivered" as shown below in the image below:

Insert your e-mail address as instructed and you will start receiving blog posts as soon as they are published.  I would like to warn you though that the posts viewed in your e-mail account might not show any graphs or images or videos - which are embedded.  In the case that this happens to you, simply click on the 'title' of the blog post and you will be directed to the original blog post on the site.



I look forward to hearing your thoughts on this new feature.  Remember, the comment section is open below and I welcome any feedback.  With that in mind, have a great day and a wonderful weekend. 

Richard Branson's Son Produces Short Films To Illustrate The Devastation By Hurricane Irma

I will keep this post brief.  Hurricane Irma ripped through the Virgin Islands along with Puerto Rico and have wreaked devastation which continues to be dealt with.  This, of course, was before the next Hurricane -- Maria -- which did additional damage.  Sir Richard Branson owns an island off of the British Virgin Islands -- Necker Island.  The island was destroyed and left only minimal structures as shown in the short (less than a minute) video shown below:

The devastation is apparent in the video.  Rebuilding the island will depend on the financial situation of Sir Richard Branson.  Simply because he owns the island.  Of course, the process might be sped up with the cash available on part by the wealth of Sir Richard Branson.



But what if the inhabitants of disaster zones do not have the 'cash flow' to rebuild in a quick manner?



The British Virgin Islands got hit equally hard as did Necker Island along with Puerto Rico.  Devastation has been widespread and the resources have been decimated which is why the process of restoring resources (electricity, water and sewage, etc.) will take a long time (some on the scale of months).  Sam Branson did a wonderful job of detailing the devastation in the video below which is just shy of 22 minutes in length.  I highly suggest watching the video - which can be streamed from the 'YouTube' site also.  Without further ado, watch the video below regarding the devastation of Hurricane Irma:

Wow.  Remember, the devastation that is documented in the video below was right due to Hurricane Irma.  Shortly after the video was made, Hurricane Maria drove through and wreaked more havoc on the Islands.  Imagine the process of restoration with no resources?  Keep the residents of the Virgin Islands and Puerto Rico in your thoughts as they struggle to rebuild their regions.  Hopefully, the U.S. congress will step up relief efforts to help speed up the restoration process.

What Does Testifying Before Congress Look Like For Secretary of Energy Rick Perry?

Energy is by far one of the top (most important) resources right behind clean water for the nation.  Therefore, the Department of Energy plays a pretty important role in providing energy to the nation and ensuring national security with respect to potential threats.  With this in mind, congress must periodically call upon the Secretary of Energy to testify in order to ensure minimal disruption in any event (threat -- natural or man-made).  The current Secretary of Energy is Rick Perry.  I wrote about his experience in a recent blog post.  Here below is his testimony before congress recently regarding the future path of the energy landscape.



There have been concerns about his ability to lead the Department of Energy during the Trump Administration.  Whenever I hear about a cabinet or top politician having to appear in front of congress, I always wonder about the process.  Additionally, I wonder about the various statements made by elected politicians and the authorities in cabinet level positions.  Without further ado, lets start with the invitation from congress to Secretary Perry which is shown below:

There are formal rules and procedures mentioned to avoid a waste of either entities time during the question and answering process.  Still, during each has a tendency to carry on which is why the hearings last so long.  Before Secretary Perry arrives, each member is given a copy of the Secretary's biography and the testimony for congress for that day.  The invitee gets to submit a statement (testimony) to prime the congress -- which will be supplied after the embedded video below.  First, lets look at his biography below:

Secretary of Energy Rick Perry Secretary of Energy Rick Perry currently serves as the 14th Secretary of Energy, and leads an agency tasked with overseeing the United States’ energy supply, nuclear defense capacity, and the 17 National Laboratories, home to many of the country’s best scientists. 

Prior to joining the Administration as Secretary of Energy, Perry served as the 47th governor of Texas. As Governor of the Lone Star State, Perry championed conservative principles that helped Texas become America’s economic engine. Under Gov. Perry’s leadership, Texas became a national leader for job creation, innovation and population growth. 

Perry’s leadership of Texas proved that economic growth and protection of the environment can be achieved simultaneously. While adding population and over 2.2 million jobs during his tenure, Texas also experienced major reductions in carbon dioxide, sulfur dioxide and nitrous oxide emissions. Despite having a rapidly growing population and one of the largest petrochemical refining industries in the world, Texas saw its climate and air quality improve. 

Governor Rick Perry is a veteran of the United States Air Force, a former farmer and rancher, and the longest serving governor In Texas history, having led the world’s 12th largest economy from 2000 to 2015. He has devoted his adult life to creating prosperity and opportunity for families. 

Perry grew up the son of tenant farmers in the tiny West Texas community of Paint Creek. The younger of Ray and Amelia Perry’s two children, he was active in scouting and earned distinction as an Eagle Scout. He was one of the first in his family to go to college, earning a degree in Animal Science from Texas A&M University, where he was also a member of the Corps of Cadets and a Yell Leader. 

Between 1972 and 1977, Perry served in the U.S. Air Force flying C-130 tactical airlift aircraft in Europe and the Middle East. He is a lifetime member of both the NRA and American Legion Post #75. Prior to being elected Lieutenant Governor in 1998, he served two terms as Texas Commissioner of Agriculture and three terms in the Texas House of Representatives. 

Perry married his childhood sweetheart, Anita, in 1982. They have two children and two beautiful granddaughters.

There is no question that Secretary Rick Perry has worked in the government at the state level as the governor of Texas.  During which time, he implemented many new energy plans at the state level which were achieved with no additional economic cost.  Whether that same style of leadership can be accomplished at the federal level remains to be seen.  He is certainly convinced (as shown in his testimony below) that his leadership style will successfully translate over to the federal level just fine.



Secretary Rick Perry gave a rather general testimony which can be translated to be (evidently) "open to all forms of energy" to move forward into the future of the United States Energy landscape.  Watch out for the following moments:


1) At around 1:54:30 Secretary Rick Perry is advised to stop "carrying on" which he states that he will "stop filibustering" -- he admits that he is wasting time.

2) At around 2:06:00 Secretary Rick Perry refers to Puerto Rico as "a country" when Ms. Castor (Florida) corrects him to instruct him that the citizens of Puerto Rico are "our people".  She also states that President Trump suffers from the same mindset -- "citizens of Puerto Rico" are not U.S. - amazing.

3) At around 2:46:00 Secretary Perry does not know what "industry tax credits -- ITC" or "production tax credits - PTC" are for industry.  He is the Secretary of the entire program?


4) At around 3:02:00 Secretary Perry starts dancing in his statements and refers to the people of Puerto Rico as "our people" -- he finally gets it -- he learned something from today's hearing.


Without further ado, below is the testimony of Secretary Rick Perry of the Department of Energy.  Here is the video which is just over 3 hours in length of Secretary Rick Perry's testimony:

The testimony above was prefaced by the written testimony shown below which was submitted to each representative prior to the hearing.  Here is Secretary Rick Perry's testimony below which was submitted to congress before his appearance:

Testimony of Secretary Rick Perry

U.S. Department of Energy

Before the

U.S. House Committee on Energy and Commerce

Subcommittee on Energy

October 12, 2017

Chairman Upton, Ranking Member Rush, and Members of the Committee, it is an honor to appear before you today on behalf of the Administration and the Department of Energy (“the Department” or “DOE”).

It’s been a couple of months since I last had the opportunity to testify before Congress. I thought it would be in order today to inform you of the goals we set once I was confirmed, and the progress we’ve made towards achieving those goals.

Upon confirmation, and during my prior testimony before both House and Senate committees, I outlined several key priorities of DOE.

Put succinctly, these priorities included refocusing the Department of Energy on its core missions:

• Promoting America’s energy security;

• Spurring innovation;

• Reducing regulatory burden;

• Restoring the nuclear security enterprise and enhancing national security through the military application of nuclear science; and

• Addressing the obligation of legacy management and nuclear waste.

I’d like to discuss these goals, and our progress towards achieving them. I will say that while we are making solid progress, there is much left to be done. There is a distinct role for Congress in helping us achieve these important goals, and I look forward to our ongoing dialogue.

In my travels during my seven months as Secretary, I have seen firsthand the scientific and technical genius we have within DOE and at our national laboratories and universities, nuclear waste sites and other facilities. In particular, I have visited the Idaho, Los Alamos, Pacific Northwest, Oak Ridge and National Energy Technology (PA and WV) National Labs. I have been to the Hanford, Waste Isolation Pilot Plant (WIPP), Portsmouth Gaseous Diffusion Plant, Nevada National Security, and Yucca Mountain sites.

I have participated in the G-7 Energy Ministers Meeting in Italy, visited the Fukushima site in Japan, led the U.S. delegation to the Clean Energy Ministerial in China, participated in the International Atomic Energy Agency meeting in Austria, and traveled to Mexico for a bilateral meeting. At each of these conferences, and at meetings in Washington, DC, I have held numerous bilateral meetings with national energy ministers and other foreign government leaders. My message has been clear. America is open for business and we are a willing partner in  making this world a safer and more prosperous place for everyone. Our leadership on early-stage energy technology research and energy security policy is sorely needed, and we intend to seize every opportunity to advance freedom and opportunity for all Americans – and all our fellow travelers on this amazing planet.

FOCUSING ON AMERICA’S ENERGY SECURITY:

There could not be a more exciting time to be the Nation’s Secretary of Energy. America is at the beginning of an energy Renaissance.

For forty years, the United States has set a goal of energy independence. In fact, this goal, and the price shocks of the 1970’s, gave rise to the Department of Energy under the Carter Administration.

Under this Administration, we have set a farther-reaching goal. We want the United States to achieve not just energy independence, but energy dominance.

This goal has impacts domestically, and across the globe.

Let me put the ‘Energy Renaissance’ in context for you:

• Oil production is expected to hit a record level next year, exceeding levels we haven’t seen since 1970.

• The United States is set to become a net exporter of natural gas for the first time in 60 years, with our trading partners in Asia, the Caribbean, Eastern and Western Europe being the beneficiaries of this boom.

• Coal production has risen 14% in 2017, and coal exports are up 55% compared to 2016 levels at that time.

• Wind and solar power now account for 10% of our national electricity capacity;

• The energy we use today is cleaner and emissions are falling.

Establishing reasonable and reliable energy discovery, development and delivery policies is putting the United States in a more stable and secure position to attend to its domestic needs.

Protecting Grid Resiliency

Energy security begins at home. America’s energy dominance depends on a reliable, resilient electric grid powered by a diverse mix of generation resources that help mitigate disruptions and enable rapid response when disruptions occur.

This diverse resource mix includes traditional baseload generation with on-site fuel storage that can withstand fuel supply disruptions caused by natural and man-made disasters. But the resiliency of the electric grid is threatened by the retirements of these fuel-secure traditional baseload resources, including coal and nuclear.

Earlier this year, I asked the staff of the Department to study the electricity markets and electric reliability. This is what I learned from their Report. Thousands of megawatts of fuel-secure generation capacity, including environmentally compliant coal and emission-free nuclear resources, have been prematurely retired before reaching full life expectancy or will be placed into retirement soon. If we lose this capacity, we jeopardize the resilience of the grid—specifically the ability of the grid to bounce back in times of major fuel supply disruptions.

As an example, the Report looked at the recent Polar Vortex—a band of very cold weather spread across much of the eastern United States in 2014. What happened is a lesson and a warning for us all. As the Committee well knows, the Polar Vortex created record-high winter peak electric demand for heating and equally high demand for natural gas for residential heating.  The market operator for much of the northeast, PJM Interconnection, struggled to meet demand for electricity because a significant amount of generation was not available to run at a time when natural gas was in equally high demand for home heating. The loss of generation capacity could have been catastrophic, but a substantial number of coal plants that were scheduled for retirement were dispatched to meet the need for electricity. Likewise, the Staff Report noted, nuclear power plants “performed extremely well during the Polar Vortex.”

Sixty-five million people within the PJM footprint could have been affected if these traditional baseload units were not available. The 2014 Polar Vortex was a warning that the current and scheduled retirements of these fuel-secure units could threaten the reliability and resiliency of the electric grid. In America, no one should have to choose between keeping their family warm and keeping the lights on. We need to be ready for the next Polar Vortex or any other shock to the system that could come our way at any time.

The DOE Staff Report warns that the continued closure of traditional baseload power plants, especially coal and nuclear, means that “States and regions are accepting increased risks that could affect the future reliability and resilience of electricity delivery for consumers in their regions.” In light of this assessment, the DOE Staff Report calls for prompt action. One of the DOE Staff Report’s chief policy recommendations is to correct distortions in price formation in the FERC-approved organized markets. Specifically, the Report states, FERC should “expedite its efforts” to improve energy price formation in centrally organized wholesale electricity markets.

In light of this recommendation, I recently exercised my authority under section 403 of the Department of Energy Organization Act by making a concrete proposal to FERC for pricing reform in the Commission-approved organized markets. Under the proposal, FERC would direct the organized markets to fully value the grid resiliency benefits provided by traditional baseload resources with on-site fuel storage capability.

In plain English, fuel security is valuable—to families, businesses, and national security. I asked FERC to change the market rules to make sure that fuel-secure generation is valued for what it is worth to our Nation – not forced into early retirement leaving the grid at risk during the next disaster. FERC has been studying these issues for years, and DOE’s own study confirms the need for prompt action.

Our proposal has attracted much interest and support. In particular, I would like to note the September 29th statement of Ralph Izzo, Chairman, President and CEO of the New Jersey-based Public Service Enterprise Group in responding to my proposal to FERC. “PSEG has long supported a national policy that would recognize the valuable benefits that nuclear power provides to our customers. We applaud Secretary Perry’s leadership and sense of urgency in announcing this initiative today to help ensure the viability of nuclear energy by recognizing the contribution it provides to the reliability and resiliency of the grid. This is an important step toward helping ensure consumers can continue to benefit from nuclear power,” Chairman Izzo said.

This proposal is just a first step in seeking to ensure that we truly have an energy policy that first and foremost protects the interests and needs of the American people. Following the recommendations of the Staff Report, the Department is continuing to study these issues and, if necessary, will be prepared to make a series of additional recommendations to improve the reliability and resiliency of the electric grid.

For years, our fuel-secure generation resources have been strangled by regulation and squeezed by pricing rules that under-value grid security. These resources must be revived, not reviled. I am taking and will continue to take action as needed to keep our diverse generation mix in place.

Our electricity supply powers our economy, lights our streets, heats our homes, and supports our way of life. As Secretary of Energy, I will not sit idly by when I see a threat to that reliability, or a reasonable course of action that is within my authority to mitigate it.

FOCUSING ON INNOVATION:

The position of energy security we Americans enjoy—and take for granted—would not have been possible without American ingenuity, and a clear focus on innovation. I am very proud of the advancements that DOE research and development has spurred. I am confident that legacy of innovation will only grow in the coming years.

Despite all the rules, red tape, misguided policies and regulations that have emanated from Washington, DC over the past 40 years, there have been two bright spots that have continued to drive American energy innovation: DOE-funded R&D, including work at the Department’s national laboratories, and the dedicated workforce in each of the Department’s program offices.

DOE’s laboratories have engaged in cutting-edge research that expands the frontiers of scientific knowledge and improves the lives of millions. While most of this innovation is in the energy field, DOE also collaborates with the health sector in conducting analytical research—including a recently launched cooperative endeavor funded by the Department of Veterans Affairs to apply our supercomputing ability to improve the quality of health care for our nation’s veterans. DOE laboratories have contributed some funding to this effort.

I have had the pleasure of personally visiting 5 of our National Labs, and I look forward to visiting each of these amazing facilities during my time as Secretary. In short, our National Labs have put a distinctly American stamp on the last century of science. We support better coordination, communication, and collaboration between the Labs, and DOE program offices will continue to push the envelope in energy research and development.

Fossil Energy Research and Development

The FY18 Budget focuses $280 million on cutting-edge fossil energy research and development to further our energy security, advance strong domestic energy production, and develop innovative clean coal technologies.

Energy Efficiency and Renewable Energy

The FY 2018 Budget funds $636 million to support research at our national laboratories to drive energy innovations in renewable energy, next-generation transportation, and energy efficiency.

Nuclear Energy

DOE remains committed to providing domestic sources of clean energy and enhancing our national security. The FY 2018 Budget provides $703 million for Nuclear Energy to support early-stage research and development and infrastructure to the continued innovation of new and improved nuclear energy technologies.

Electricity Delivery and Energy Reliability

DOE serves as the lead agency for Emergency Support Function 12 (ESF-12) under the National Response Framework. As the lead for ESF-12, DOE is responsible for facilitating the restoration of damaged energy infrastructure. This is a top priority function of the Department.

During Hurricanes Harvey, Irma and Maria, and the weeks following these unfortunate events, we have worked with industry and Federal, state, and local partners to facilitate response and recovery. At the height of our recovery efforts after Harvey and Irma, our industry partners had more than 60,000 personnel from all 50 states in the field.

Currently, we are involved in the restoration efforts in the Virgin Islands and Puerto Rico. More than two dozen technicians from DOE and the Western Area Power Administration have been in the Virgin Islands, restoring critical power supplies to hospitals, airports and ports, and we have additional personnel in Puerto Rico. We will continue to support the work needed to restore power to the Virgin Islands and Puerto Rico until the job is finished.

Regardless of the event that threatens to disrupt the electric power system, DOE and its dedicated partners in private industry will be there to help.

Protecting the electric grid also entails dealing with man-made threats.

The Budget also includes $42 million for energy delivery system cybersecurity in the Office of Electricity Delivery and Energy Reliability, with a renewed focus to take steps to make a difference within two years in the cybersecurity of our Nation’s power grid. Our budget funds early stage activities that improve cybersecurity and resilience of the grid in order to harden and evolve critical grid infrastructure. We focus on early stage R&D at national laboratories to develop the next generation control systems and components, devices and systems with engineered-in cybersecurity features; and we fund a new activity to develop a continuous monitoring capability that will significantly increase our awareness and ability to prevent and respond to these types of events.

Additionally, all power generation, regardless of the fuel, relies on the power grid to delivery electricity to our homes and businesses around the nation. The Budget provides $120 million to support research and development at the national laboratories to develop technologies that strengthen, transform, and improve energy infrastructure so that consumers have access to reliable, secure, and clean sources of energy.

In addition to R&D, the Department examined grid reliability and resiliency in detail in the Staff Report on Electricity Markets and Reliability made public in August. We continue to engage FERC, NERC and other stakeholders on these issues.

REDUCING REGULATORY BURDEN:

On January 30, 2017, the President issued EO 13771, which directed agencies to be prudent and financially responsible in the expenditure of funds, from both public and private sources, and to alleviate unnecessary regulatory burden placed on the American people. In addition to the management of the direct expenditure of taxpayer dollars through the budgeting process, it is essential to manage the costs associated with the governmental imposition of private expenditures required to comply with Federal regulations.

Subsequently, on February 24, 2017, the President issued EO 13777, which directed agencies to lower regulatory burdens by implementing and enforcing regulatory reform and to establish

Regulatory Reform Councils chaired by a Regulatory Reform Officer (RRO) to oversee implementation of EO 13777 at the agency. DOE has established a Regulatory Reform Officer to oversee the implementation of regulatory reform initiatives and policies to ensure that the agency effectively carries out regulatory reforms, consistent with applicable law. And on March 28, 2017, the President issued EO 13783, which directs agencies to review all agency actions in the interest of promoting the clean and safe development of our Nation’s vast energy resources with particular attention to spurring the development of oil, natural gas, coal, and nuclear energy resources.

In order to meet these Administration-wide deregulatory commitments, the agency is currently reviewing all existing regulations, orders, guidance documents, policies, and any other similar agency actions. DOE is also committed in the long term to take a continuous look at regulation in order to lower regulatory burdens on the American people.

ENHANCING NATIONAL SECURITY:

As a participant on the National Security Council, the Department has a unique role in our Nation’s security. I undertake these responsibilities with the utmost gravity.

For more than 70 years, a cornerstone of our national security strategy has been our nuclear deterrent. By any measure, the strategy of nuclear deterrence has served us and our allies well. It facilitated the collapse of the Soviet empire, and with it, the dire threat it posed to freedom, stability, and peace.

Under the leadership of the President, the Department of Energy through the National Nuclear Security Administration (NNSA), and in partnership with the Department of Defense, seeks to strengthen our deterrence capabilities. We aim to make these capabilities more robust, flexible, and resilient than ever, so we can meet 21st century challenges.

We are currently working to advance key programs designed to extend the life of existing U.S. nuclear warheads by replacing them with systems that use modern technologies. Our work will also help us replace our aging nuclear security infrastructure – our extensive network of laboratories, plants, and sites. Some of these sites date back to the Eisenhower Administration and are in need of updates.

At the same time, through its non-proliferation and naval reactors efforts, NNSA is a leader in our nation’s efforts to ensure these weapons do not fall into the hands of rogue regimes or terrorists and maintains the superiority of propulsion systems for our Navy’s submarines and aircraft carriers.

In short, through our work we’ll seek to deter those who are not friendly to the United States, while convincing our friends to put their full trust and confidence in us as steadfast allies.

ADDRESSING THE OBLIGATION OF LEGACY MANAGEMENT AND NUCLEAR WASTE:

Fulfilling Legacy Cleanup Responsibilities

Every Secretary of Energy, upon confirmation, is met with the magnitude of the Department’s cleanup mission.

It is our obligation to clean up the environmental legacy of the very weapons and programs, sites and communities that helped us win World War II and the Cold War.

We have made great progress, and I’ve seen this first hand at several of our Environmental Management sites this year.

There is no more plutonium on the Hanford site in the State of Washington. All 20 tons of leftover plutonium have been shipped out of Hanford.

Significant progress has been made on key sections of the Waste Treatment plant, and demolition of the Plutonium Finishing Plant is scheduled for completion this year or early next year.

Seventeen (17) billion gallons of contaminated groundwater have been treated.

Work along the Columbia River has advanced to a level that a portion of land no longer needed by the Department has been transferred to the community.

There is much more work to be done, and we will need your help to achieve this important environmental management goal.

My direction has been to put DOE on a final path to achieving the cleanup mission across our enterprise sooner, safer, and at less cost to taxpayers.

We will continue to press forward with tackling excess facilities at Portsmouth, Ohio; Paducah.  Kentucky; and Oak Ridge, Tennessee.

We will continue our progress on the sections of the Hanford Waste Treatment Plant necessary for the Direct Feed Low Activity Waste (DFLAW) approach, which is vital to beginning tank waste treatment at Hanford.

We will commission and start up clean-up operations at the Savannah River Site on the South Carolina-Georgia border, as well as complete design and begin construction of the Oak Ridge Mercury Treatment Facility.

Addressing the Imperative of Nuclear Waste Management 

The Department of Energy has another obligation - to advance solutions for the long term and secure storage of spent nuclear fuel and high-level waste. There are more than 110 sites around the country that are storing these materials.

We have a national security obligation to come up with a long-term solution, finding the safest repository or facilities available. The recent natural disasters and the ongoing threat of terrorism should heighten our resolve to secure this material in the safest possible facilities and as expeditiously as possible. The American people deserve a solution to this problem and we can no longer kick this can down the road.

In addressing all of our cleanup and storage obligations, we also have a compelling responsibility to American taxpayers. Therefore, the Administration proposes to terminate the Mixed Oxide (MOX) Fuel Fabrication Facility project. There is another approach – dilute and dispose – that is less expensive, has far lower risks, and can be implemented decades sooner than the MOX approach. I urge this Committee to help us make this important transition.

Conclusion

Mr. Chairman, and all the members of the Committee, I want to thank you once again for inviting me to share my vision about how we can make America more prosperous and energy secure.

Americans have always come together to meet the great challenges of our time. We all want to protect the environment. We all want to prosper economically. I am here to tell you, from my experience as the Governor of Texas for 14 years, that we can – and will – have both. Similarly, we at the Department of Energy are coming together with our many stakeholders to find solutions to the many challenges before us.

I look forward to working with every member of this Committee and the entire Congress to realize the President’s vision of energy dominance, support the creation of more high-paying jobs for American workers, and produce more reliable and affordable energy for all Americans.

Thank you very much and I look forward to answering any of your questions.

In the months to years (next couple of years) we will see how this testimony translates into national security and resources for each of the residents of our nation.  By the sounds of the testimony in the video above coupled with the words above, Secretary Rick Perry and President Trump still are a ways off from being able to completely promise safe resources and keep the United States at the forefront of technology moving toward a more sustainable way of living.  Each need to think hard about the direction of other rising nations.  How much investments in renewable energy?  How much money in basic research?



The current administration appears to be stuck in the mindset of moving the nation back toward a time when oil and coal were 'booming' -- the dominant sources of energy.  Having an ample supply of electricity as back up being fueled by both coal and nuclear sounds reasonable.  Although, in a future where cleaner technologies are starting to play a more dominant role, our nation needs to prioritize its spending toward meeting those needs.  Currently, that thought is not in place.

Puerto Rico Aid Should Not Be A Partisan (Political) Issue

The recent Hurricanes Irma and Maria have decimated parts of Puerto Rico.  Puerto Rico is part of the United States.  The island is not a "country" by itself as suggested recently by our Secretary of Energy Rick Perry.  Regardless, we have a moral obligation to help fellow residents to recover and provide sufficient relief immediately following a disaster.  I received a rather disturbing message in my e-mail box regarding the relief effort in Puerto Rico from 'Politico Energy' earlier this week which is shown below:

CONCERNS RAISED OVER PUERTO RICO FRAUD: A group of House Natural Resources lawmakers, led by Chairman Rob Bishop, sent letters Tuesday to FEMA and the FBI seeking information about alleged mishandling by local officials of emergency relief supplies in Puerto Rico. "Allegations that local elected officials are distributing life-sustaining FEMA emergency supplies based on political loyalty is deeply disturbing," they wrote. "Any persons misappropriating FEMA emergency supplies should be prosecuted to the fullest extent of the law." The lawmakers want briefings from both agencies by Oct. 23.

Hearing announced: Bishop announced the committee would hold an oversight hearing on the Puerto Rico response efforts Oct. 24. Energy and Commerce subcommittees are expected to announce similar sessions this week.

McCaskill seeks her own investigation: Sen. Claire McCaskill, the top-ranking Democrat on the Homeland Security Committee, called for a bipartisan investigation into the federal government's response to the string of recent hurricanes. Letter here.

The very possibility that such a disparity for food relief could exist should make anyone sick to their stomach.  Of course, maybe this is expected after the recent comments made by President Trump over the last few weeks which are shown below:

Each citizen of the United States and its territory deserve to be supported through their respective natural disasters.  We are a nation who do not leave its citizen out in the cold to die...at least that is what we hear from various politicians.  If this is the case, then we have an obligation to support the residents of the Virgin Islands along with the residents of the island of Puerto Rico.



On Wednesday of this week, the governor of Puerto Rico visited President Trump at the White House.  The shift of leaving the residents of Puerto Rico out in the cold has evidently shifted due to unforeseen forces (political -- Congressional Support behind the scenes) motivating the President to change his position regarding funding the rebuilding of lost electrical infrastructure.  This was highlighted in this morning's email from 'Politico Energy' below:

CHATTER ON REBUILDING PUERTO RICO'S GRID: During an appearance with Trump on Thursday, Puerto Rico Gov. Ricardo Rosselló floated the idea of using public-private partnerships to help rebuild the island's electric grid. Rosselló said he hoped to "rebuild a much modern, much stronger platform, and not only have Puerto Rico have energy but actually be a model of sustainable energy and growth towards the future." Trump replied: "You were talking about rebuilding your electric plant long before the hurricane; you've been wanting to do that for a long time. So maybe this is a reason that we can do it. And we'll help you and we'll all do it together."

Side note: Seems like Trump is referring to the electric grid when he refers to the "electric plant."

Patience is a virtue: Trump said it would be a "period of time" before electricity could be restored on the island given its electric infrastructure had been "totally destroyed." The president floated one potential policy idea: "It would be wonderful if you could have underground wire. It makes it a lot better in these storms." (Side note: Underground wires didn't fare so well during Hurricane Sandy in New York and it would hugely expensive for the whole island).

Rosselló promises corruption crackdown: "If there is a public official that is purposefully mishandling the food that should go to the people of Puerto Rico, there is going to be some hell to pay," he said.

These suggestions sound great.  Let us see what surfaces in reality for the residents of Puerto Rico and the Virgin Islands.  Every day there seems to be a new revelation that the current natural disasters are causing a great partisan divide.  Actually, the culprit of the divide is the promise that the Trump Administration made to the public to reduce 'federal support' -- i.e., federal regulations, federal spending, federal workers (number of employees).  The result of which are with the current disasters which have plagued various parts of our nation.  Funding for relief and recovery have been cast by this administration into a partisan battle as highlighted in the excerpt below:

 HOLD UP: Senate Majority Whip John Cornyn has placed a hold on Russell Vought's nomination to be deputy director of the Office of Management and Budget unless he gets more funding for Texas hurricane relief, Axios reports. That comes as Florida Sen. Bill Nelson said Thursday he'd also placed a hold on Vought's nomination after the administration kicked funds for his state's citrus growers to a later disaster relief package.

Hold up...this is "political hijacking" of a nomination based on funding relief efforts for American citizens.  The practice is unethical and immoral on all levels.  There is an unspoken commitment to the residents of the United States to provide relief and rebuilding funding for the future generations of this country.  Lets stop letting partisan politics get in the way of repairing the damage to our nation from these natural disasters and heal in order to move forward as a nation -- united.

Natural Disasters Hit, What Happens to School Students?

I imagine work and school are not a top priority when a Hurricane comes through a city of state.  Additionally, if a fire burns across a large geographical area affecting the residents resources.  Although, after the initial shock wears off (which is subjective for each resident), what happens to students?  I was thinking about this consequence after reading the excerpt below from 'Politico Education' this morning:

CALIFORNIA WILDFIRES DISPLACE TENS OF THOUSANDS OF STUDENTS: California wildfires forced about 132 schools to close as of Tuesday, displacing nearly 63,000 students, according to data from the California Department of Education. That's just 1 percent of the Golden State's total student population. But for some schools - like those located in Napa County's five school districts - students have been out of the classroom for almost two weeks.

- Napa County students were supposed to return to school today. But as staff members on Tuesday prepared for their arrival, they quickly realized that the air quality was dangerous, choked with smoke and ash. "Some staff said they weren't feeling well, so we released them," said Janet Tufts, superintendent and principal of Howell Mountain Elementary School District. The five school districts in Napa County have canceled school for the rest of the week, said Barbara Nemko, superintendent of the Napa County Office of Education. They'll be adhering to strict air quality guidelines to determine whether it's safe for students to return. They've been distributing air masks, replacing air filters, shampooing carpets and washing down desks, hallways and playgrounds. And they'll likely have to do it again this weekend, since schools are closed until Monday.

- School is pretty much the main social hub for kids who live in the rolling hills of rural Napa County, said Susan Eakle, who teaches kindergarten through second grade for Pope Valley Union Elementary School District - a school district with just one school, five teachers and 58 students. Many of the parents work for vineyards, and the fires have hit during harvest season. The nearest grocery store is about a half-hour away and the nearest Walmart is about an hour away, said Ken Burkhart, who is principal and superintendent of Pope Valley Union Elementary School, in addition to being a full-time teacher. The school wasn't in an evacuation zone, but two of the school's five teachers weren't able to return this week because they were evacuated, he said. Burkhart said that when he was evacuated from his home, he drove his RV to school and stayed in the parking lot.

- Napa County schools are now figuring out how to make up for two weeks of lost learning time. But they're also bringing in counselors and psychologists to help students and staff dealing with trauma and stress. "Evacuations are a big deal for kids," Burkhart said. "They'll remember it for the rest of their lives." School officials are still assessing exactly how the wildfires have affected students and their families, and whether they sustained damage or lost their homes. But even if families didn't see any damage, the stress caused by evacuations, fire and smoke have affected everyone. "These students have been exposed to something that not many of us will see," Nemko said. "You can see the fire from their neighborhood, even if it's not in your neighborhood."

Parents go to work during the day and children go to school - right?  That is the logic that is instilled in kids during growing up.  After a terrible disaster hits an area, the following questions naturally arise in each persons mind:



1) What happens if my house is destroyed and I have no means to live in an area after a disaster?

2) What happens when the place I work at is destroyed?

3) What happens when the school does not exist anymore -- has been wiped out?

4) How does our family return to a 'normal life'?

5) How do we make up for lost education?



The first four questions are immediate concerns for each member of the family to consider after a natural disaster hits their place of residence. Whereas the fifth question is one that is typically not entertained unless the disaster has completely destroyed the school.  Although, when students are displaced from school either for psychological or physiological reasons, their educational journey can be greatly affected.



Puerto Rico...



In a previous post, I briefly stated the observation that after Hurricane Maria hit the island of Puerto Rico, nearly 80% of the crops were decimated -- stripping the island of an important food source.  Not to mention that the 95% of residents were without electricity.  Upon starting the recovery process, the fifth question above -- school students -- must be addressed.  Can they catch up on missed material?  What is the function of education during a time of disaster recovery?  Maybe the students are better served by assisting with the recovery process to feel part of the recovery?



I also mentioned in that previous post that I had a friend who is finishing up Medical School down in Puerto Rico.  This is his final year.  During which, he is predominantly occupied with "rotations" in different subdisciplines in medicine.  He is training to be a psychiatrist, but part of his medical school education requires him to rotate to other sub-specialties such as 'gynecology' or 'family practice', etc.  Which brings me to the point -- what is the function of education during a time like this?



Interestingly enough, he had a test two weeks after Hurricane Maria hit Puerto Rico in Dallas, Texas.  Therefore, he needed to come back to the states on a humanitarian flight to make the exam.  During his stay, he received a call from his medical school administrative office asking him if he could do a few of the remaining rotations in the states rather than on the island.  Especially, since he was missing time on his current rotation to take a 'clinical exam' -- Step 2 exam.  He agreed to find rotations state side.



To close, a recent article in the New York Times details that one of the most needed forms of assistance now on the island of Puerto Rico is that of 'Psychiatrists' at his medical school - Ponce University.  Hurricane Maria's adverse impact on my friend's remains to be seen.  With all of the problems occurring on the island, is there anything medical school to return to?



In Conclusion...



The last aspect of our lives we consider in a disaster is the educational process.  I am not proposing that from now on we place a greater emphasis.  I am bringing to light the fact that education in its entirety in relation to the world we live in.  Educating the young during the disaster recovery might be a missed opportunity rather than worrying about "missing school".  Regardless, as a society, school is secondary to survival.  At the very least, consider the disruption to your life (in all aspects) given the tragedy of experiencing a natural disaster.  Lets keep those who have suffered and continue to suffer from the disastrous consequences recently in our thoughts as we progress forward on a daily basis.  Life is precious.  We are larger than just ourselves.  Community education is powerful as is university education.  Until next time, have a great day!

How Much Trash Would Be Required To Fill The Great Wall Of China?

Staten Island (New York, USA) has grown to be a waste repository of trash over the last few centuries.  The following excerpt appeared which astonished me in a recent article from the website 'Nautilus' titled "Reinventing Staten Island":

After World War II, the bursting city of New York found itself with a trash problem. In 1948, the city started officially dumping its trash into the marshes and waters of Fresh Kills. What became America’s first landfill was meant to be temporary, but it stuck. By 1955, it was the biggest landfill in the world—indeed, at 2,700 acres, it was the biggest human-made structure in the world. By 1991, the landfill contained 150 million tons of tightly packed garbage in more volume than could fill the Great Wall of China. Fresh Kills was wetland no more.

Specifically, the last sentence stood out among others.  Which spurred the following questions in my mind:



1) How did a region manage to let 150 million tons of garbage collect in a single landfill?

2) What is the volume of the Great Wall of China?

3) How does the volume of the Great Wall of China compare to the stated value of 150 million tons?



The answer to the first question is complex and beyond my reach for an answer.  I would defer the question to the politicians of the great state of New York.  As for the next two questions, the overall interest which arose in my mind was to compare the stated value in the article to the actual (or approximate) volume of the Great Wall of China.



Basically, if I calculated a volume using approximate methods, how would that number (pounds of trash) compare to the value of 150 million tons?  I will show below how to calculate the volume of the Great Wall of China and compare the answer to the stated value above.

How Big Is The Great Wall Of China?

When a reader encounters an enormous number such as "150 million tons" -- naturally the enormity will be difficult to comprehend.  Which is why the process of 'dimensional analysis' is useful to cast an incomprehensible number into at least a semi-comprehensible number.  The metric which the author chose in the excerpt above was the Great Wall of China shown below:

Source: History Channel

The dimensions of the Great Wall of China can be found by asking a search engine such as 'Google' the following: What are the dimensions of the great wall of china?  The answer to which is shown below as a list of possible web links:

In this particular case, I chose to use the approximate values given in the descriptions of the first three links shown above.  Specifically, for the length of the wall, I used the value of 13,170 miles in length.  Wow!  I did not realize that the Great Wall of China was that long.  Of course, I have never visited the Great Wall of China, therefore, I had no real guess.  Parts of the winding wall are shown below which span a large length:

Source: Wikipedia

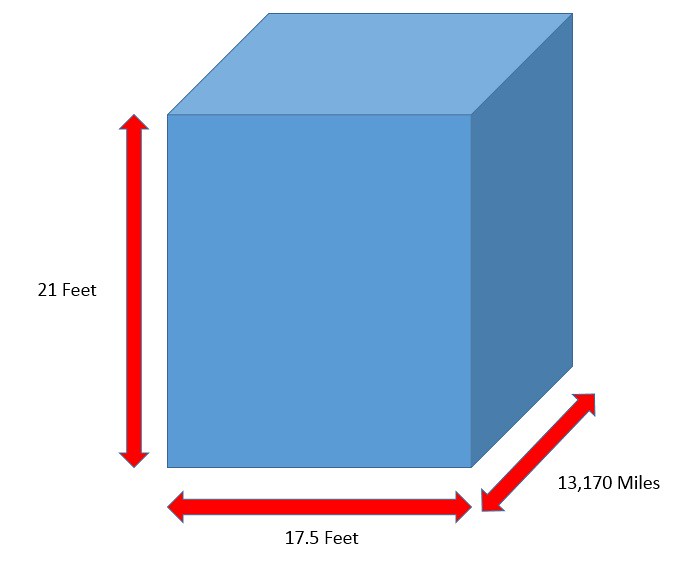
There are two remaining measurements that are needed to calculate the volume of the Great Wall of China -- the 'Width' and 'Height' of the wall.  In the description contained in the image, the base of the wall is around 19.6 feet in width, whereas, at the top, the width is around 16 feet.  There seems to be a large amount of variance.  Given the size and the age of the structure, that is to be expected - possibly.  In the image below, I show a 'trapezoid' with the values given above of the varying width if the wall with height:

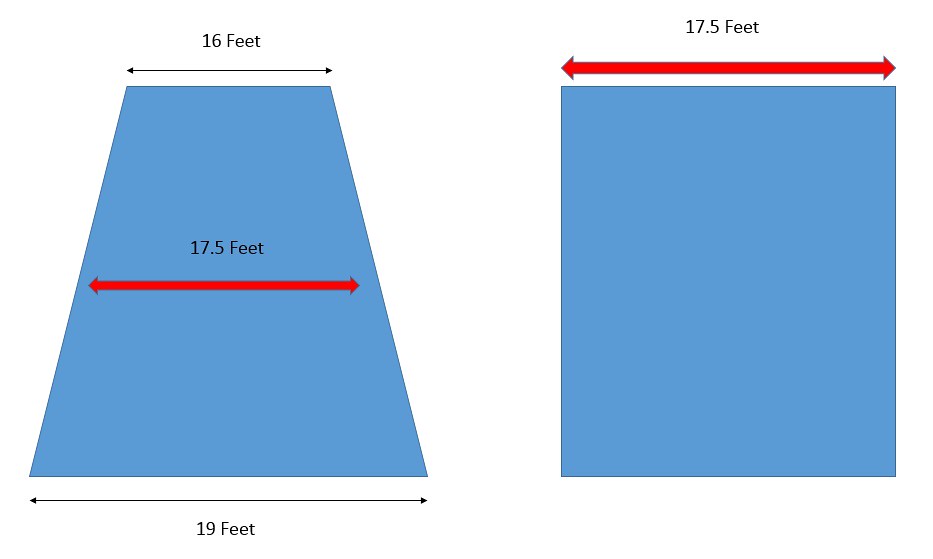
With any dimensional analysis problem, the important point is to approximate the parameters (unless you have an exact value) and calculate.  The problem can be turned into an 'optimization' problem where we re-evaluate the value of the parameters and then try to be more accurate in approximating the correct values of the dimensions and recalculate.  For now, an initial value is important to try to find an initial answer.  As I mentioned above, the length of the wall is stated to be around 13,170 miles.  Therefore, below I show the values of the Great Wall of China which will be used to calculate a volume:

Note: first that there are different 'units' of measurement for different parameters.  For the length of the wall, I express the value in 'units' of 'miles' instead of units of 'feet.'  For the purpose of calculating the volume, the preferred unit will be the 'yard'.  In order to convert from units of 'miles' to units of 'yards' the conversion factor needs to be known.


Again, asking a search engine such as 'Google' can yield an answer.  If you type in the following question: How many yards in a mile?  The following answer (conversion factor) appears:

The conversion factor from units of 'mile' to 'yard' is therefore used to convert the length of the Great Wall of China from 13,170 miles to the equivalent number of yards as shown below:

Converting the length of 13,170 miles into 23,180,000 yards is required to ensure that when the volume is calculated below, the final units will be expressed in 'cubic yards'.  The only way to accomplish the conversion is to ensure that all three dimensions are in equivalent units of 'yard'.



In the cartoon image of the wall above, the width and height of the wall are expressed in units of 'feet' while the length is expressed in units of 'mile'.  The unit conversion from 'mile' to 'yard' has been accomplished above.  The remaining unit conversions needed are of width and height.  In order to do so, the conversion factor from 'feet' to 'yard' needs to be known.  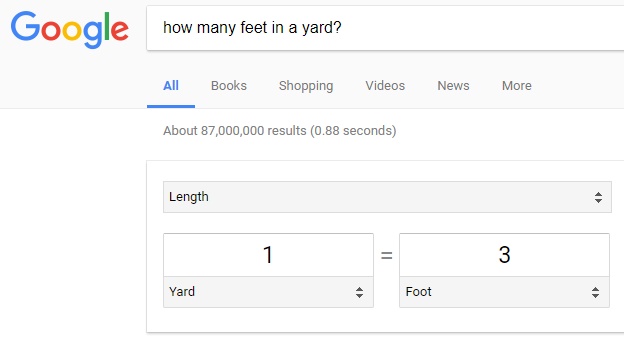Next, we follow the method above of asking a search engine such as 'Google' the following question: How many feet in a yard?  The answer is shown below:

Now that the conversion factor from units of 'feet' to 'yard' is known, the following unit conversions of both the 'width' and 'height' of the Great Wall of China can be accomplished as follows:

... and the height of the wall is shown below:

All three dimensions of the volume of a rectangle have been converted to the 'common' unit of 'yard'.  Next, an expression for the volume of a rectangle needs to be obtained.  Shown below is an expression for the volume of a rectangle:

The volume of a rectangle is defined by the area of the face of a rectangle multiplied by the length extended back into space.  I define this based on the cartoon image above showing all three parameters.  The length of the Great Wall of China is known as are both the width and height.  To start to find the volume, first the calculation of the area of the rectangle (wall -- represented as a 'cross-section').  An expression for the area of a cross-section (or rectangle) of the wall is shown below:

From the converted values into units of 'yards' above, the following width and height can be easily plugged into the expression for the area of a cross-section of the wall as shown below:

The area of a cross-section of the Great Wall of China is 40.8 square yards as shown in the calculation above.  In order to calculate the volume of the Great Wall of China, the area is multiplied by the length of the wall as shown in the expression below:

The total volume contained in 13,170 miles of the Great Wall of China is 946,000,000 cubic yards!  That seems to be an enormous (and incomprehensible) volume.  The above calculations satisfy the second question initially asked in the blog post.  Specifically, what is the volume of the Great Wall of China.  In the current blog post, the Great Wall of China is used as a metric to compare the enormous value of trash (in weight) of 150 million tons -- which was dumped over decades onto Staten Island.



How do these two numbers compare in magnitude?



That is difficult to say in the current form.  Why?  Because, the value of the volume of the Great Wall of China is expressed in units of 'cubic yards' while the enormous amount of trash is expressed in units of tons.  A weight cannot be compared directly to a volume.  Although, through the relation of a compounds 'density' - the amount of weight in a given volume -- the volume of trash may be determined as you will see in the next section.

Volume Of A 150 Million Tons Of Trash

The amount of trash which has accumulated onto Staten Island over the last few decades is around 150 million tons.  According to the author of the excerpt, that amount is enough to fill the Great Wall of China.  After showing the excerpt, I asked three questions regarding this enormous (and incomprehensible) statistic.  The third of which is stated at follows:



3) How does the volume of the Great Wall of China compare to the stated value of 150 million tons?

As I just mentioned at the end of the last section, the route toward comparing the volume of the Great Wall of China is through comparing two enormous volumes.  The first volume is that of the Great Wall of China, which was calculated to be 946,000,000 cubic yards.  In order to compare this huge volume to the weight of 150 million tons of trash, a conversion from a weight to a volume needs to be accomplished.

An object (in this case a pile of trash) has a certain composition of material.  The material has a weight and takes up a certain amount of space.  The density of such a material is defined as the weight of a material divided by its volume (which is taken up by a material).  In the case of trash, a search engine can be asked the following question:

The average density of trash is around 1,400 lbs/cubic yard.  Now that the density of trash in a landfill is known, the next step is to check the 'units'.  Notice how the density of trash is expressed in units of 'lbs/cubic yard".  That is pounds per cubic yards.  Which means in order to use the value of density in the conversion, the weight of the trash must be converted to units of 'lbs' from 'ton'.  To start, the weight of the trash pile is expressed in scientific notation as shown below:

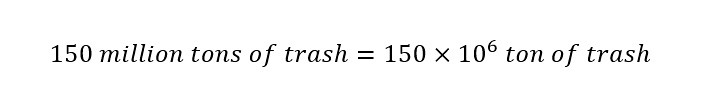
In order to convert the weight of 150 million tons of trash into units of pounds, the conversion factor must be obtained.  If 'Google' is searched, the following answer appears below:

For every ton of trash, there are 2000 pounds.  The conversion between units is easily accomplished as shown below:

The answer indicates that a 150 million tons of trash is equivalent to 300 billion pounds.  Next, an expression for the relationship of mass to volume of matter must be obtained through the concept of 'density' -- which is shown below:

Since the density is known of the trash in a pile (or landfill), the expression can be rearranged to yield the volume of 300 billion pounds of trash.  The expression is rearranged to solve for volume by dividing mass by density.  This expression works for all matter which occupies a given space.

Plugging in 300 billion pounds for 'mass' and '1,400 pound/cubic yard' for density yields the following expression for the volume of trash as shown below:

The answer can be interpreted as the trash on Staten Island will take up a volume of 214,000,000 cubic yards.  That is 214 million cubic yards of space given the compaction density of 1,400 pounds/cubic yard.  Now that the volume of trash is known, the amount of the Great Wall of China (which can be filled up with trash) can be determined.  This is accomplished by dividing the volume of trash by the volume of the wall as shown below:

Wow.  That was unexpected.  According to the calculation, only 214 million cubic yards of trash will only fill the Great Wall of China 22.6%.  That is just under a quarter of the entire space in the Great Wall of China.

Conclusion

The initial statistic from the author of the excerpt given at the beginning of the blog post was the following:

By 1991, the landfill contained 150 million tons of tightly packed garbage in more volume than could fill the Great Wall of China. Fresh Kills was wetland no more.

After reading this statement, you would be led to believe that the volume of trash that accumulated on Staten Island was greater than 946 million cubic yards -- the volume of space inside the Great Wall of China.  Although, the calculated percent volume which would be filled with 150 million tons of trash was only 22.6% of the volume of the Great Wall of China.  Which leads to the following question:



Why is there such a difference in results?  How did the author arrive at the statement?  What parameters did she use in the calculation?



The questions above arise from the clarity (or transparency) of the stated statistic.  This happens way too often in the media.  Transparency is the best bet.  I will e-mail the author and ask her how she arrived at the following result which led to the statement in the excerpt above.  The exercise above shows the ease with which a person without a science background can 'fact check' or 'statistic check' a written statement in the media.  Go on and try to find a 'metric' (such as the Mercedez Benz Superdome) to compare the enormous value of trash in the excerpt above.  Leave your result in the comments section below.  Until next time, have a great day!






Related blogs can be found here:


Dimensional Analysis Of Statistics And Large Numbers - Index Of Blog Posts


What is dimensional analysis?


How many trash carts can be filled with 80 billion pounds of trash?


How many people would be killed if 1,485 pounds of Fentanyl were distributed onto the streets in the U.S.?

What Is Dimensional Analysis?


Was The Recent Oil Spill in China The Largest In History?


LimeBike Dockless Bikeshare Riders Travel A Distance Of 13,000 Miles In Just Over 3 Weeks?

How Many Cigarettes Can You Roll With 18,000 Pounds Of Marijuana?


How Many Turkey's Are Served On Thanksgiving Day? How Many People Served?


How Much Trash Would Be Required To Fill The Great Wall Of China?


How Many Birds Per Minute Can Be Processed On A Single Line At A Poultry Processing Plant?


Hurricane Harvey Drops Enough Rain On Houston To Fill 560 Dallas Cowboy Stadiums

If Technology Fails, Use Basic Math Skills - Count Manually!!

How Much Water Is Contained In All Oceans Around The Globe?

Teacher Starts A Conversation Rather Than Lecturing From High In The Ivory Tower

This semester, my partner -- Dr. Kayla A. Kaiser -- is teaching a class called "Science 100" for the 3rd time at California State University at Northridge.  Big Deal right?  Well, actually, this year she changed her methodology to see if there is a difference.  What methodology?  In short, she started a conversation through providing a meal for each of the 24 students while cementing sustainable measures by listening.  The result of which remain to be seen, but below is a "letter" from Dr. Kayla Kaiser to her students regarding her intention.  Initially, the results have been extremely positive.

Backstory: First Assignment

Before I post her "letter" to her students, I must give you a small backstory to her new methodology.  Instead of the tradition manner of teaching this course -- which is to teach the students "modules" which are composed of subjects with a wide range, such as "sustainability" to "are there aliens on other planets?".  She decided to give a first assignment to her class: write down your favorite family recipe.



Whether that recipe was from a special meal or if the meal is your favorite meal made by a member of your family.  The students were then tasked to go and retrieve the recipe and write down the correct description -- which included ingredients and procedure for making the meal.  Each week, every Monday and Wednesday, Kayla will spend around 5 hours cooking one of the recipes for the class of 24 students the next day.  Challenges include the interpretation of the recipe, transferring the food the next day to the class, and learning how to correct for potential mistakes in the interpretation process.  The experience so far has been a great learning experience for Kayla.  I can attest to this since I see her going through the process in our kitchen twice a week.

"Letter To My Students"

Without further ado, below is the "letter" from Dr. Kayla Kaiser to her students discussing her strategy for changing her methodology this semester as opposed to previous classes:



Before the semester started, I asked myself: What is the one thing I can do for my SCI 100 students to help them feel welcome at CSUN, learn more effectively, and connect with each other?  My brain told me to feed you healthy, fresh meals.


I attended an eLearning Institute this summer to learn about all kinds of online tools and games to get students excited about learning.  But I also thought about some of the studies my dad (who is a teacher) told me about that the two things that make the biggest difference in student success are:

1. free breakfast and free lunch
2. free clothing 

 
By Philipp Guttmann - Own work, CC BY-SA 4.0, Link



In order to achieve the "self-actualization" that is the goal of higher education, you must feel that your physiological needs (food, clothing, shelter) are met.  Then you should feel that the university is a safe place and that you belong here.  Next, you must be challenged and rise to the challenges to develop self-esteem.



I wrote in my application to the eLearning institute that I wanted to increase "social belonging" in my classroom and "cultural relevancy" in my lessons.  The food project is meeting both of these goals. The food project has allowed me to practice "cultural humilty."  Cooking cuisine outside the breadth of my experience has taken me back to being a student, to the feelings of uncertainty every student experiences when asked to carry out an unfamiliar task.  Sometimes professors can forget what it feels like to learn new tasks.



Failing at pozole has allowed me to model resiliance.  I had a feeling it wasn't right, but served it anyway, to criticism and rejection.  Sometimes you have to turn in an assignment even if it isn't your best work, because the deadline has arrived.  Also, after you get a low grade on an assignment, it means that you belong here.  A failing grade is not a sign that you should give up.  Even though you get knocked down, your education is worth getting back up and moving on to the next assignment.  If you're not failing, you're not risking.

When you take risks you learn that there will be times when you succeed and there will be times when you fail, and both are equally important.  -- Ellen De Generes

I appreciate that you have all given me the opportunity for "co-learning," where we are constructing a collaborative cookbook.  I hope you're all enjoying the opportunity to connect with each other and learn about each other's culture through food.  Each time I cook one of your recipes, I imagine the generations who have survived on this Earth eating that particular dish and I am filled with gratitude for the abundance that you all have brought to our University.




------------------------



Stay tuned for more results of this teaching method to come!!

Hurricanes Harvey and Irma Hit USA While Politicians And Agency Directors Still Deny Contribution Of Climate Change

In the aftermath of both Hurricane Harvey and Hurricane Irma, the remaining question lingering in everyone's mind is the following:


What was the contribution of climate change to these two disastrous hurricanes which ravaged our infrastructure and led to the very unfortunate loss of life?


Now, not everyone is entertaining this exact or variants of the stated question.  With every explanation, there will exist deniers who just do not want to entertain the facts which science lay out and seem to explain certain phenomenon.  Undoubtedly, the current hurricanes are increasing in severity due to climate change.  The exact contribution from us (humans) might not be quantifiable, but that does not mean that the contribution is not real.



Furthermore, as both geographical regions in the United States start the process of rebuilding their regions, urban planners along with government employees would be well served to consider climate change in future planning efforts.  Otherwise, future storms will bring more havoc on local, state, and federal resources.  Lets review briefly what the two hurricanes brought to local, state, and federal resources - briefly - below.

Climate Change Is Not Partisan

Contrary to popular belief, climate change sees no partisan borders.  Whether a person, region, government is rich or poor, well established or new, weather patterns are what they are.  And part of the existing situation is attributed to the past.  This might seem debatable to either side.  Although, I would suggest looking at photographs of recent floods and the increase in severity of each and try to convince me that change is not on the horizon.



Hurricane Harvey did considerable damage to the Houston area.  Remember that President Trump voted to defund FEMA and Flood mapping research a few months ago.  Here is a short video from an article out of the Washington Post titled "The cruelest insult to Harvey and Irma’s victims" which sheds light onto potential issues pre-Hurricane Harvey:

After viewing the short video, I cannot help but wonder the following questions:


1) Why was Houston not equipped with stronger weather infrastructure to avoid potentially rising sea levels or handle large amounts of rain?

2) Why were so many chemical industries and oil industries allowed to locate to a 'flood plain' which amounts to a potential disaster in the event of rising sea levels or power outages?


Who allowed the build out of Houston?  Some one knows the answer to these questions.  There are city council members with information which could answer these questions.  I wonder what those city council members are thinking right now?  I wonder how many of them were displaced due to Hurricane Harvey?  I wonder how many of the original designers/builders still live in the Houston area?  Probably not many.



Unfortunately, asking such questions now makes little sense.  What does make sense is to think globally as time moves forward and the rebuilding phase commences.  As Eugene Robinson writes in the Washington Post article cited above, the time to think wisely is now:

This is precisely the moment when scientists at the EPA, the National Oceanic and Atmospheric Administration, the National Weather Service, NASA and other agencies ought to be laser-focused on climate change. They should study the characteristics and impacts of this season’s hurricanes to better understand what changes global warming has wrought thus far. And I’m confident they will do so — unless their work is hampered by political hacks.

Climate change never should have become a partisan issue in the first place. There is no red or blue spin on the fact that humans have burned enough fossil fuels since the Industrial Revolution to increase the concentration of carbon dioxide in the atmosphere by more than 40 percent; or that carbon dioxide traps heat; or that global land and ocean temperatures have shot up; or that Arctic ice is melting; or that sea levels are rising. These things are directly measurable and true.

Global warming cuts no slack for political affiliation — as Republican Govs. Greg Abbott of Texas and Rick Scott of Florida now should humbly acknowledge.

The time is now.  Unfortunately, our energy secretary (Secretary Rick Perry) is an ardent climate change denier feels differently as shown in the following excerpt taken from a CBS news article:

"We can line up scientists on both sides of this," he told CBSN's Stephanie Sy, but "this is not the time to be having this conversation." At this moment, he said, it's time to focus on helping victims recover from the damage wrought by Harvey.

"Everyone wants to run to the climate change debate, but that is very secondary at this particular time," he said.

Energy Secretary has a track record of ignorance on climate change and pushing agendas which are counter intuitive toward the direction in which science is headed.  I wrote a blog post discussing his qualifications recently which should be read after finishing this article.  His ignorance is pretty serious considering the amount of people who are without power and those who lost their lives during Hurricane Harvey.  I am astounded to say the least and disappointed.



Another critical agency which has seen changes in funding due to our current President is the Environmental Protection Agency.  EPA Director Scott Pruitt also has a track record which prevents him from serving the nation effectively.  Therefore, as we have seen during both storms, loss of life and damage beyond repair is starting to appear.  Further, EPA Director Scott Pruitt holds the same view as Secretary Rick Perry on discussing the subject of climate change during a storm search and rescue along with recovery.  Basically, both hold the position that climate change is not directly related and can wait until a later time to come into play (or discussion).



These views might hold up under fire except that both of these Administrators are hell bent on defunding their agencies -- taking money from the public (Federal agency) and rerouting the funding to the private sector.  Both of these men are heavily backed and supported by industry.  One of the critical issues among many are the construction permitting and building licenses which are issued by these agencies.



The EPA and DOE play a large part in ensuring that corporations practice safe and reliable services through enforcing regulations set by the government.  Many residents feel like regulations are "job killers", but the reality is that the industry mantra is to profit at the cost of safety of the consumer (bluntly said).  Members of the Trump Administration refuse to discuss proactive measures -- like disaster preparedness and consumer safety.  What is more preferred is to discuss "job killing regulations".

Federal Funding Is Critical For Disasters

After two hurricanes, one would think that government officials would be willing to discuss the devastating effects of natural disasters and their potential causes.  One of which is climate change.  A contributor to say the least -- in elevating the severity of the storm -- not the main cause of course.  With the President looking to defund federal agencies, the money available to be proactive in future disasters remains limited.



Further, research into potential solutions to future storms is out of the question.  Not to mention (as I did above) the ability of the federal agency to regulate corporations to practice safety in the workplace (for workforce) and provide high quality products (consumer safety).   In order to change the current direction of the Trump Administration, the first step is to stop denying the existence of climate change and accept it -- in order to move forward.  Below are two excerpts which drive home the need to move forward and stop letting climate change become a "partisan" issue.



Here is an excerpt from the Mayor of Miami -- Tomas Regalado:

Miami’s Republican mayor called on President Donald Trump and the head of the Environmental Protection Agency Friday to acknowledge that climate change is playing a role in the extreme weather that has slammed his city and the continental U.S. this summer.

Speaking from Miami’s Emergency Operations Center in downtown, where the city’s senior public safety and political authorities will ride out Category 4 Hurricane Irma this weekend, Mayor Tomás Regalado told the Miami Herald that he believes warming and rising seas are threatening South Florida’s immediate and long-term future.

“This is the time to talk about climate change. This is the time that the president and the EPA and whoever makes decisions needs to talk about climate change,” said Regalado, who flew back to Miami from Argentina Friday morning to be in the city during the storm. “If this isn’t climate change, I don’t know what is. This is a truly, truly poster child for what is to come.”

On top of that realization, 'Politico Energy' tip-sheets include the following regarding the mixed views of politicians in Washington D.C. in the wake of Hurricane Harvey and Hurricane Irma:

ALL QUIET ON THE CLIMATE FRONT: Even as the double whammy of Hurricanes Harvey and Irma offers the U.S. an up-front glimpse of the types of devastation the world faces due to a warming climate, Democrats are largely holding their fire on Republicans, Pro's Emily Holden and Elana Schor report . Instead, they appear to be heeding the warnings of several of President Donald Trump's Cabinet officials that discussing climate change with large swaths of land still underwater would be insensitive. "The response to Hurricanes Harvey and Irma thus far has been more muted, likely in part because of a desire to keep the focus on immediate disaster relief," said Trevor Houser, former energy adviser to Hillary Clinton's presidential campaign.

Democrats say there will be opportunities to explore the linkage between extreme weather and manmade climate change moving forward. "We have a lot of time to make that point, and I think we also have a lot of legislative opportunities as we look at reauthorizing flood insurance and funding the disaster relief," Sen. Sheldon Whitehouse , one of staunchest climate hawks, said. Environmental advocates have hit Trump's inaction on climate change online, but have shied away from criticizing Democrats. "The truth is, I'd settle for politicians not talking about climate at all, and instead actually doing something," Bill McKibben, founder of 350.org, said.

Tone shift at the White House? Tom Bossert, Trump's homeland security adviser, told reporters Monday that the cause of both devastating hurricanes is "outside of my ability to analyze" but he acknowledged a need to bolster flood and coastal defenses threatened by rising seas and powerful storms. "We continue to take seriously the climate change, not the cause of it, but the things that we observe," he said. "What President Trump remains committed to is making sure that federal dollars aren't used to build things that will be in harm's way later or that won't be hardened against the future predictable floods that we see." While those words may offer hope to some, ME would note Trump has erased climate considerations from government processes, nixed flood standards for federal projects, withdrawn the U.S. from the Paris climate change agreement, pulled back a regulation to limit carbon dioxide from power plants and halted funding to help poor nations adapt to new weather extremes.

More money needed? Asked if the administration would put more money into agencies like FEMA and EPA, Bossert expressed openness to requesting additional funds - "We'll put money in as money is needed to address the need," he said - but added "right now we have plenty of resources to get through this."

Irma could've been even worse: Even as millions lost power during Hurricane Irma, the head of the state's largest utility said outages could've been even worse if Florida Power & Light Co. had not spent $3 billion to improve the energy grid, POLITICO Florida's Bruce Ritchie reports. "With this kind of storm what I can tell you is, we would be facing a much longer restoration" without the work, FPL President and CEO Eric Silagy said Monday.

Again, the politicians are missing the big point.  The following points need to be highlighted by the news for future disasters:


1) President Trump voted to defund FEMA, which included funding research for flood plane proned areas.

2) Senators have voted "no" for disaster relief funding -- even, in some instances for their own state -- to stand on principles (i.e. no increase in debt ceiling).



These are critical issues  which affect large (hundreds of thousands) amounts of U.S. citizens still today.  Just because the rebuilding and restoration of both Texas and Florida are not covered by the national news does not mean that the geographical areas are not in serious need of assistance.  There are houses still under water and areas without power along with areas covered in toxic chemicals which the EPA refuses to acknowledge.



Here are two aftermath effects of ignoring climate change and defunding Federal Agencies along with reversing Obama era environmental regulations:

Checking in on Texas: EPA reported late Monday that 35 of the 2,238 drinking water systems affected by Harvey remain shut down, while 35 of the 1,219 wastewater treatment plants in affected countries also remain inoperable. The agency further said it had "directed potential responsible parties or has independently started collecting samples at the 43 Superfund sites to further confirm any impacts from the storm" and said additional assessments continue at two sites - San Jacinto Waste Pits and U.S. Oil Recovery. In addition, Reuters reported federal officials are cleaning up spills of oil and chemicals spilled from a dozen industrial facilities in the aftermath of Harvey.

Yikes: Water testing arranged by The New York Times from two Houston neighborhoods showed alarmingly high levels of bacteria and toxins. Tests from the Briarhills Parkway in the Houston Energy Corridor showed levels of E. coli at levels four times of what's considered safe, while Clayton Homes public housing development downtown showed concentrations of E. Coli more than 135 times healthy levels, as well as elevated levels of lead, arsenic and other heavy metals. The EPA said Monday that 40 of 1,219 waste treatment plants affected by Harvey were not working.

And...

 EPA LAUNCHES PROBE INTO ARKEMA INCIDENT: Officials at EPA have requested information from Arkema to help them ascertain whether the chemical company properly followed Clean Air Act safety regulations before Hurricane Harvey. EPA asked in its letter , obtained by ME Monday, for a response from the company within 10 calendar days of receipt. Among the information sought is what the company did before the storm to prepare for potential flooding and loss of electricity, as well as the quantities of chemicals stored on site. Several chemical containers at the Crosby, Texas, facility caught fire after the hurricane deluged it with water.

Unfortunately, the actions by the EPA is only in response to the popular news coverage of the disasters brought by the two devastating Hurricanes recently.  Furthermore, the Clean Air Act which was enacted by the Obama Administration has been ignored and not enforced by the Arkema chemical plant.  Which resulted in the release of large amounts of volatile chemicals when hurricane harvey hit Texas.  EPA Director Scott Pruitt should be ashamed of himself for standing up in front of the public on television and stating the the EPA has everything under control.  With 40 waste treatment plants not working and exceedingly high levels of bacterial organisms in the water, people are at high risk of disease.



Not to mention the Superfund sites which are another source of extremely high levels of chemicals -- some of which are unknown.  The result is complete chaos brought to you by the Trump Administration.

Conclusion

When a nation is reversing the course of decades worth of environmental regulations enacted to protect consumers and our resources, the result is chaos.  Which is were we are at presently.  At any given time, a natural disaster can occur in this great nation and the implications of a lack of federal funding will be completely apparent.  Why do the great people of the nation believe that the President cares about their safety?  With the direction of giving money to big corporations while defunding federal agencies, you get the present situation -- a lack of preparedness.  Over time, this will get worse if nothing is changed.  The excerpts above clearly show that the issue of climate change is becoming a partisan issue when the issue should not be.



Now with the devastation caused by yet another Hurricane - Maria in Puerto Rico, the time has come to ask ourselves where we would like to be as a nation.  Currently, the crops that were destroyed are not recovered in Florida much less the newly destroyed land in Puerto Rico.  There are areas which are not being covered by the news which remain ravaged and without resources.  How prepared are you for a disaster?  How do you feel about federal funding?  Do you follow FEMA status or updates on a daily basis?  There is an app you can download to get FEMA updates on various parts of the nation where disasters are occurring and where relief is being directed.



Regardless of your position on climate change, the effects of climate change are real and noticeable.  In the future, the storms will worsen and the frequency will become greater.  Talk to your local representatives and ask them to consider climate change to be real and the need to study the effects in a given geographical area.   This is an ongoing discussion here on this site and in national news, so stay tuned.