Alright, how about after viewing the following tweet shown below:
When I first laid eyes on the tweet above, I instantly wondered the amount of water which would result from melting 4000 tons of snow. In the blog post below, I will show how I tackled the problem of determining the amount of water in 44 feet of snow fall.
Snow To Water Ratio?
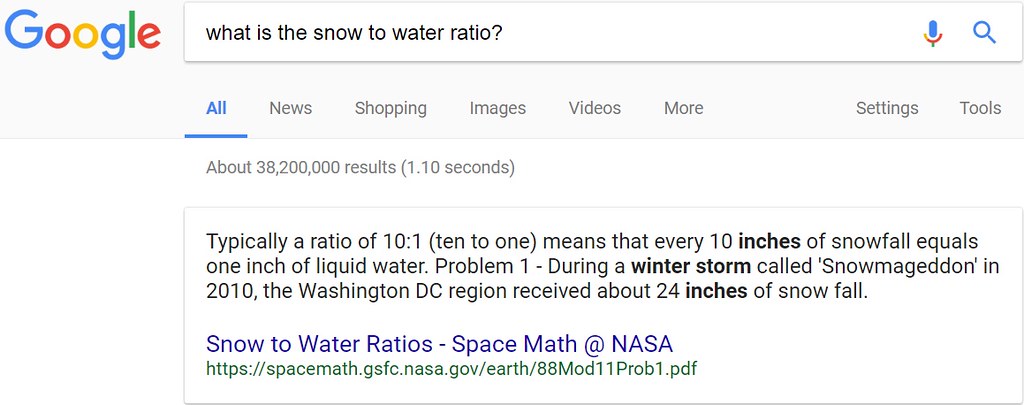
In order to understand the quantity of water that will result from any given snow fall, the snow-to-water ratio needs to be known. How does a person find the snow-to-water ratio? Answer: ask Google.com as shown below:
For the purpose of the blog, the ratio of '10:1' -- meaning, for every 10 inches of snowfall, there will be 1 inch of rain water which results. The document highlighted in the box above is an excerpt of a 'PDF' from the website "spacemath.gsfc.nasa.gov". Upon reading the entire document, the ratio actually is temperature dependent as shown below in a table:
Source: spacemath.gsfc.nasa.gov
For the purpose of simplicity, the value which will be used to calculate the amount of water produced in a given rain fall will be -- 10:1. Since the value for the amount of snow is given above which was taken from the article, the only remaining task is to calculate the amount of water contained in 4000 tons of snow. Right off the top, with the weight of the snow known, a quick calculation would reveal the following regarding 4000 tons of snowfall:
In 4000 tons of snow fall, there will be roughly 400 tons of water. That is the easiest answer to arrive at. Although, most people do not think of quantities of water expressed in units of 'ton'. Therefore, in order to make sense of the answer above, a number of unit conversions will need to be made. In order to do these conversions, the conversion factors must be known.
Where does a person find conversion factors?
How many pounds are in a ton?
How many grams are in a pound?
How many gallons are in a gram?
How many liters are in a gallon?
The last question should be confusing at first sight. In order to make sense of the quantity of water in a given space or weight, the density of water is used as a conversion factor. To arrive at the final amount of water in gallons, we need to ask 'Google.com' each of the questions above to get conversion factors to be used in the calculations.
Lets start with the first question: How many pounds are in a ton? The result of a search is shown below:
The answer indicates the following conversion factor shown below:
Which is that there are 2000 pounds in a ton. With this value, the amount of tons of water (400 tons) can now be converted to pounds of water as shown below:
There are 800,000 lbs in 400 tons of water. The next question is now ready to be asked: How many grams are in a pound? The result is shown below:
The answer of the search reveals that there are 454 grams in a pound of water. I rounded the value up for memory purposes -- I remember that there are 454 grams in a pound. The number 454 is equated to a large Chevy big block engine. With the above conversion factor from pounds to grams, the next conversion is possible as shown below:
The number keeps getting larger as we convert down to smaller quantities. This is an indication that we are on the right track toward a final answer. Typical density conversion factors are expressed in units of 'gram/mL'. For water at room temperature, the value of the density is 1.00 gram/mL. Before we perform the last conversion, the last question should be queried: How many liters are in a gallon ?
The result of the search reveals the final conversion factor needed as shown below:
Now, we can finish off the final conversion and arrive at the number of gallons of rain water that is contained in 4000 tons of snow fall as shown below:
Wow!!! There are 96 million gallons of water in 4000 tons of snow fall. In the article above, the snow fall that was reported was the quantity of snow that was removed off of the streets in the town. The effort was directed to relieve the residents of the town who were trapped by the unusually enormous amount of snow fall that fell in a given storm. The quantity of 4000 tons of snow resulted from 44 feet of snow fall. These numbers are staggering to consider at first sight.
World's Largest Swimming Pool
The volume calculated above is enormous and incomprehensible when passed over in a news article. In order to understand the magnitude of the snow fall further, a metric can be used to cast the large volume of water into perspective. Previous readers can probably predict what metric that is appropriate given a volume of 96 million gallons of water.
If you guessed that the metric chosen would be formerly known as the "World's Largest Swimming Pool" -- then you would be correct. The largest known swimming pool was formerly the swimming pool located down at the San Alfonso del Mar resort (in Chile) which holds a total volume of 66 million gallons of water and is shown below:
Source: Huffington Post
Since the volume of water (66 million gallons) is known from the website, determining the number of swimming pools which could be filled with the water from the snow fall of 96 million gallons is straightforward and is shown below:
The answer indicates that for the total volume of water which fell as snow fall in a storm, the enormous formerly "World's Largest Swimming Pool" could be filled once and still have 29.7 million gallons of water remaining. Nearly, 1.5 times. Now the amount of snow in 4000 tons can be realized with an easy visual of the enormous swimming pool located at the resort in Chile.
Conclusion...
Upon first viewing the 'Tweet' shown above, the average person might just scroll on down and overlook the enormous amount of water which fell in a storm as snow. In the post above, I have shown how to ask the question: How Much Water Is In 44 feet Of Snow? I have always wondered what the snow to water ratio was. After calculating the amount of water and casting the number in a light (a perspective) with the "World's Largest Swimming Pool," the fact that the national guard was called in should be no surprise. That amount of snow is too much for the average resources of a small town. Luckily the national guard had the infrastructure and man power to help out. Calculations like those above help readers (you and me) in understanding the enormous effort needed to clear the roads and help out residents during a giant storm such as the one reported in the news story highlighted above.
Until next time, have a great day!

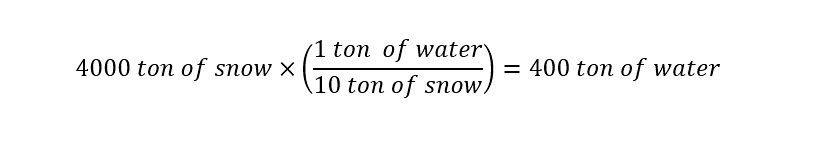

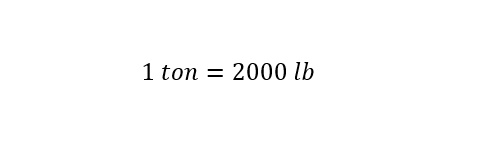
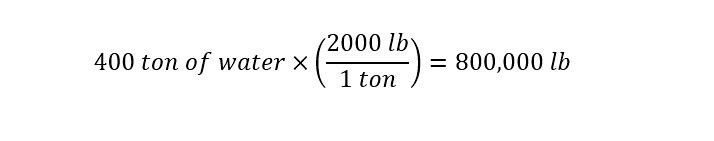



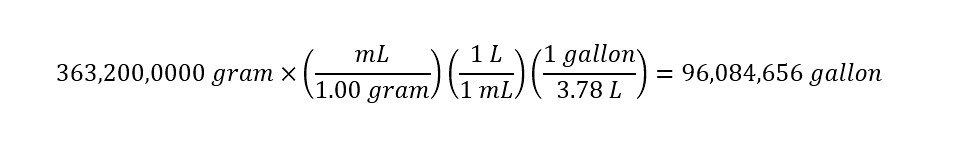

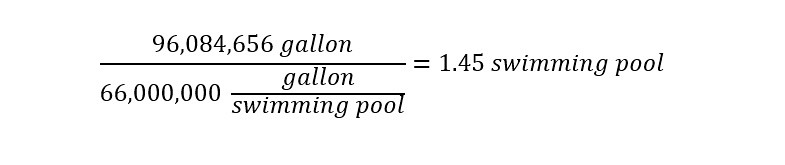
No comments:
Post a Comment