The technique that is used to solve for the amount of paint needed to cover a given surface is called 'Dimensional Analysis'. Dimensional Analysis is extremely useful in viewing the world. I know, I know that the statement is too general. Understanding the usefulness of using dimensional analysis is beneficial in a variety of situations. Don't believe me? One of the goals of the blog (Mike Thinks) is to liberate the reader by teaching them to use the method to bring clarity to difficult problems. We can use a rather simple example to illustrate my point.
How Much Paint Is Needed To Paint A Wall?
How about using dimensional analysis to decide the amount of paint needed to cover an area (893 square feet area) with paint. How would we determine the amount of paint to purchase in advance to accomplish the task? This is an example given in a college chemistry course by my wife.
Right about now, you are probably wondering how the question was stated on the quiz given by Dr. Kayla Kaiser. Shown below is the question regarding the amount of paint required to paint a given surface:
As you can see that an answer is given to the problem. The answer is written out in a conversion format. That is starting from the area required to paint and ending with the amount of paint required to paint that area -- in this case the answer is 28,400 gallons. That is a huge amount of paint. When I first heard the amount of paint, I had to ask the amount of area that was required to paint. Of course, I am a chemist and am curious. The amount of paint is excessive for the required area. How do I know this? Let me explain.
First, in the question, the conversion factor is given for a given volume of paint to a 2 Dimensional surface. Do you see? Here: a gallon (volume) of paint covers a square yard (2 dimensional surface). Second, the area that is needed to be painted is given = 843 square feet. Additionally, a conversion factor 3ft = 1 yd (3 feet equals 1 yard). What is left? In science lingo - - just plug and chug dude -- with a calculator.
But seriously, how do we approach the problem without a calculator -- an estimation?
Without a calculator, we can come close to an answer to the entire problem. Or at least we can determine what 'order of magnitude' the answer should reside within. How? The answer lies in looking at each of the given numbers in the question. First, lets look at the two conversion factors given. Both are shown below:
First, looking at the conversion from feet to yards (1yard = 3 feet), there is an ample amount of useful information within this statement. With a little bit of mathematical manipulation to each side, we can arrive at the amount of square feet equal to a square yard.
To walk the reader through the above manipulations, first list in an equality the desired conversion. In this case, 3 feet is equal to 1 yard. Second, to get to 'squared' units -- squared feet -- this is an area (two dimensional) with units to the second power or squared. Next, if we square the unit (feet or ft, yard or yd), we need to also square the magnitude (the number in front of unit) -- in this case the number 3. We are left with the conversion that in a square yard, there are 9 square feet -- as shown above in the last line.
Next, we can manipulate the conversion factor of volume to an area given in the question. How much paint (a volume) covers a given surface (two dimensional area). Below I show the conversion given in the question -- which is 1 gallon of paint is required to paint 15 square yards:
The second line is shown to convert the units of area to feet from yards. In the previous calculation the conversion was from yards to feet. This conversion is needed since the desired area to be painted is expressed in units of 'square feet or sq. ft'. Converting any area to square feet will help our analysis. As you can see, no calculator has been needed so far. Lets review what has been shown.
Since 15 square yards can be painted with a single gallon, we need to know the equivalent square feet. A one-step calculation (multiplication) reveals that 9 multiplied by 15 equals 135. With a single gallon of paint, we can paint 135 square feet. If we were to multiply both sides by 10, we get the following: 10 gallons of paint will adequately cover 1,350 square feet. Again, all this without a calculator thus far.
Why is this analysis important without a calculator?
If we recall the initial image that contained the question and a student's answer (the wrong answer), we can compare the two answers. The student got an answer of 28,400 gallons are needed to cover 843 square feet. Is this correct based on the few calculations that we have carried out thus far. I hope that you said -- NO WAY. Why?
With a single (1) gallon of paint, we can cover 135 square feet. Do you agree? With 10 gallons of paint, we can paint 1,350 square feet -- Right? Well, the value we were asked in the initial question falls into the range of the two values (1 and 10 gallons).
Therefore, without a calculator, we can estimate that the correct amount is less than 10 gallons and more than a single gallon. Now, how much paint is required?
Using the same two conversions above, we can calculate the amount of paint required to cover an area of 843 square feet. My calculation is shown below:
Is that calculation not simple or what? Take 843 and divide the number by 9 and then follow with another division by 15 to arrive at the final answer of 6.2 gallons. The amount of paint needed to paint an area equal to 843 square feet is 6.2 gallons of paint. Imagine that, our value falls within our range of estimation (previous mathematical manipulations).
Remember how I started the blog post asking about the amount of paint required to cover an iMAX movie screen. Based on the calculation, how hard would that calculation be? Not hard at all should be your answer -- Right?
How Much Paint Is Required To Paint An IMAX Screen?
The process by which to calculate the amount of paint required is given above. At the moment, the only unknown is the size of an IMAX movie screen. Where does one find the answer? I know how about asking google? I asked google and was given an assortment of links to various answers. The answer I liked most was the simplest. A website called "LFexaminer.com" gave me the two values that I asked for and in a simple manner. According to the website, the average area in square feet for an IMAX screen is 1,884 square feet. Now that we have the average area, we can just repeat the calculations above, which I show below -- substituting a new value for area:
Does the answer make sense based on the above calculations? Of course! The area of the screen is 1,884 square feet. Remember, for 10 gallons of paint, an area of 1,350 square feet could be covered. Therefore, the value (gallons of paint required) has to be greater than 10 gallons. And the answer is greater than 10 gallons. How about if we look at the largest IMAX screen in the world. How large is that screen? Again, according to the website 'LFexaminer.com' the dimensions of the largest IMAX screen in the world (which is located in Australia) are (97 feet X 117 feet) -- WOW! That is a screen area of 11,310 square feet. Again, using the method above, the calculation is shown below:
Oh my goodness, 84 gallons of paint. Does that make sense based on the values above? Yes, based on the above calculations for 843 square feet, a screen the size of 11,310 square feet should be over 10 times the amount required for the original area. The number is 14 times the amount required and the area is just over 13 times the original area. This illustrates the power of comparing various numbers to validate range or order of magnitude in which the value should lie within.
Conclusion
The calculations above illustrate the power of using dimensional analysis to reason out numbers. What do I mean by this? How could dimensional analysis be useful in real life? According to the example above, dimensional analysis could save a person money the next time you plan to paint a surface (wall of a house, wall of a building, etc.) The next time that you look at a movie screen or the wall of a building, try to guess the amount of paint that would be required to paint the surface.
Just think, you will never be bored again. You now have the ability to guess the amount of paint required to paint a given sized surface. All that you need to remember are the three conversion factors (3 ft = 1 yd & 1 gallon = 15 square yard & 1 square yard = 9 square feet). Whatever the square feet just divide by 9 and follow by 15 to get the amount of gallons required.
Numbers are very important. Units give numbers meaning. When numbers are reported, using dimensional analysis can give you a better understanding of the magnitude of the reported number. Just last week, I wrote a blog post on the amount of gas stored at Aliso Canyon Gas Facility. I was gracious to have a reader comment and ask me to clarify the assumptions. In the comment section, you will find a reader's comments. Why do I bring this example up?
In the above example (with paint), a reader might ask for clarifications. What type? Such as how is the conversion factor of 1 gallon required to cover 15 square yards. How is that determined? There are light coats of paint and then heavy (perceived as a double coat). I believe that my wife got that value from a paint store. But that is not really important. What is important is the an answer is reached based on the information provided. Then, the reader can evaluate the answer.
The largest mistake that chemistry students make is not paying attention to the values of the parameters along with the wording of the problem. If a person maps out the problem correctly, an answer can be reached without a calculation. At least an estimation can be reached which will give the student some insight. Too often, students and people in life are looking for answers or validation to problems in the form of answers. Given a set of skills (logical thinking and reasoning), a person has the power to arrive at a reasonable solution without a large amount of effort.
Try to calculate the amount of paint required for a given surface. Or compare the numbers in the blog post. Play around with a calculator a little (for 10 minutes or so) and you might find a little confidence to tackle an issue that has been bothering you through this indirect form of empowerment.
Have a good evening!
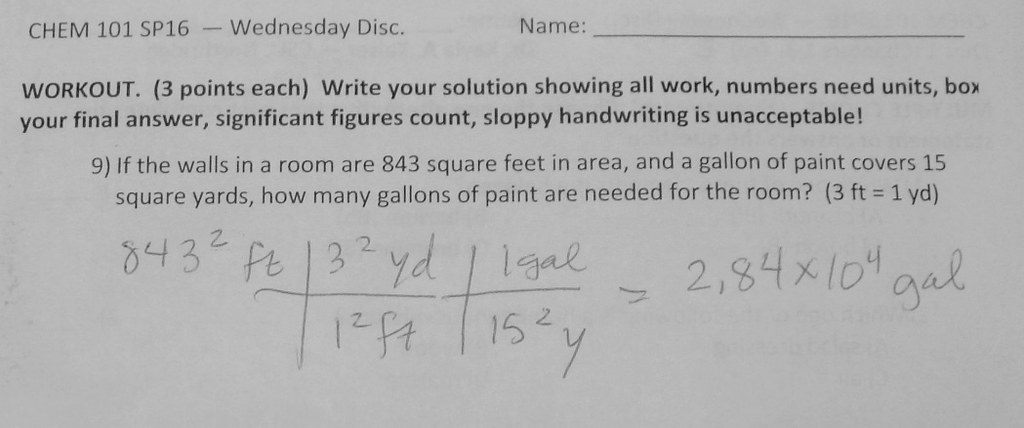
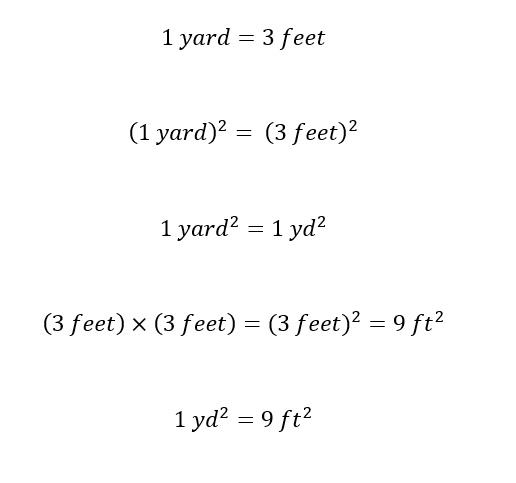


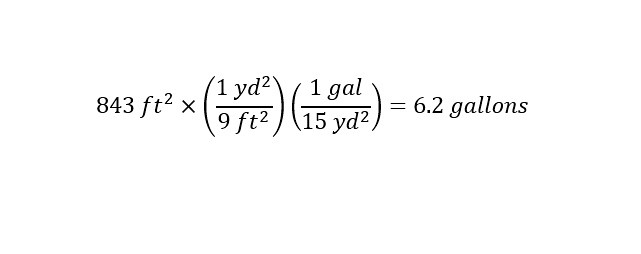


No comments:
Post a Comment